以下はGeoGebraによる作図です。
点Pを動かして見てください。本来は点Pが3次関数上と変曲点における接線上にあるときは接線が2本引けるはずですが、0.01の狂いもなく上になければ2本の接線が描かれません。これを手動で合わせるのは無理です。格子点には自動的にスナップしてくれますので、3次関数上と変曲点における接線上でかつ格子点である点にPを合わせてみてください。座標で言えば、極大点(-1,2)、極小点(1,-2)、点(2,2)、点(-2,-2)、点(-1,3)、点(1,-3)です。
接点を\ \ とおく.
$y’=3x^2-1$より,\ 点Pにおける接線の方程式は
この直線が点$(1,\ k)を通るから{y=k}$の共有点の個数が①の実数解の個数である. {3次関数では接点の個数と接線の本数が一致する
接点が不明な問題では,\ 接点を文字でおいてとりあえず接線の方程式を作成する.
接点(a,\ f(a))におけるf(x)の接線の方程式 y=f'(a)(x-a)+f(a)
点(1,\ k)を通るから,\ これを接線の式に代入すると,\ ①が導かれる.
①の意味合いが重要である.\ kは定数なので,\ ①は変数tについての方程式である.
tは接点のx座標なので,\ tの3次方程式①は接点のx座標を求める方程式}である.
さて,\ \uwave{3次関数では\ (接点の個数)=(接線の本数)}が成立する.
よって,\ 接線の本数を求めるには,\ 接点tの個数,\ つまりは①の実数解の個数を求めればよい.}
結局,\ 実数解の個数問題(定数分離型)}に帰着するわけである.
3次関数において接点の個数と接線の本数が一致することの証明}を示しておく.
下線部程度の記述でも十分だと思われるが,\ これを示しておくとより丁寧な解答になる.
3次関数f(x)=ax^3+bx^2+cx+dと2点\ x=α,\ β\ で接する直線y=mx+nの存在を仮定する.
整式では「接する\ ⇔\ 重解」}であることに注意する.
2点\ α,\ β\ で接するならば,\ f(x)-(mx+n)=a(x-α)^2(x-β)^2}\ が成立する.
ところが,\ 左辺は3次式,\ 右辺は4次式となるから,\ これは矛盾である.}
よって,\ 3次関数と2点で接する接線(二重接線)は存在しない.
3次関数では接点の個数と接線の本数が1対1で対応する}といえるわけである.
逆にいえば,\ 4次以上の関数では2点以上で接する接線をもつ可能性がある.
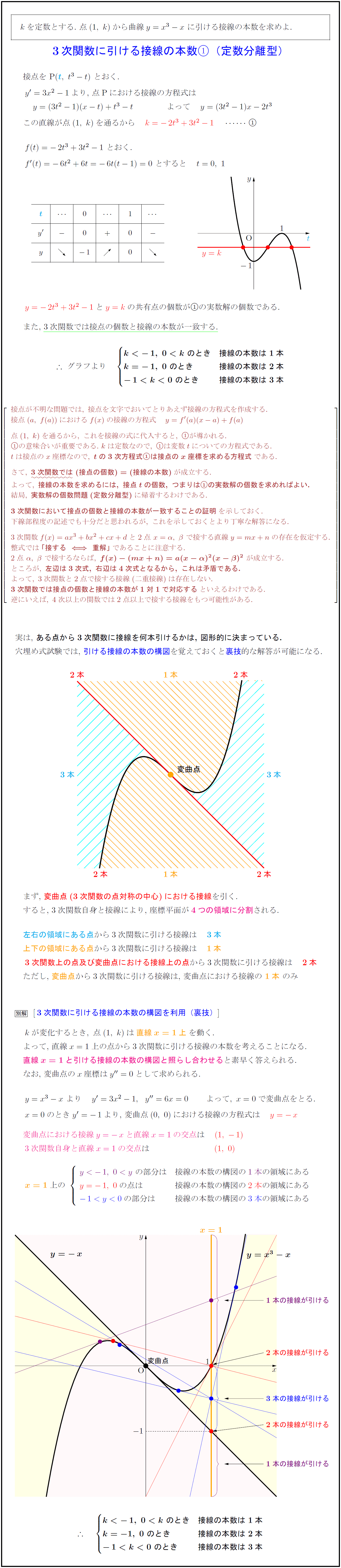
実は,\ ある点から3次関数に接線を何本引けるかは,\ 図形的に決まっている.}
穴埋め式試験では,\ 引ける接線の本数の構図を覚えておくと裏技的な解答が可能になる.
まず,\ 変曲点(3次関数の点対称の中心)における接線を引く.
すると,\ 3次関数自身と接線により,\ 座標平面が4つの領域に分割される.
左右の領域にある点から3次関数に引ける接線は 3本
上下の領域にある点から3次関数に引ける接線は
3次関数上の点及び変曲点における接線上の点から3次関数に引ける接線は
ただし,\ 変曲点から3次関数に引ける接線は,\ 変曲点における接線の\ ,3次関数に引ける接線の本数の構図を利用(裏技)]
$kが変化するとき,\ 点(1,\ k)は直線x=1上を動く.$
よって,\ 直線$x=1$上の点から3次関数に引ける接線の本数を考えることになる.
直線$x=1}$と引ける接線の本数の構図と照らし合わせると素早く答えられる.
なお,\ 変曲点の$x$座標は$y”=0$として求められる.
$y=x^3-x\ より y’=3x^2-1,\ \ y”=6x=0 よって,\ x=0で変曲点をとる.$
$x=0$のとき$y’=-\,1$より,\ 変曲点$(0,\ 0)における接線の方程式は y=-\,x}$
変曲点における接線$y=-\,x$と直線$x=1$の交点}は $(1,\ -\,1)}$
3次関数自身と直線$x=1$の交点}は
$x=1上の\ の部分は & 接線の本数の構図の1本}の領域にある
\ y=-\,1,\ 0}の点は & 接線の本数の構図の2本}の領域にある
\ -\,の部分は & 接線の本数の構図の3本}の領域にある

