(\log_ax)^n\,の形がある関数は\log_ax=tと置換する}しかない.
対数関数分野でも同種の問題を取り上げたが,\ 本問は3次関数に帰着するので微分の出番となる.
\log_aM^r=r\log_aM}\ が成り立つが,\ (\log_aM)^r=r\log_aMは成り立たないので注意する.
一般に,\ 置換したときは置換後の文字の範囲に注意する}必要がある.
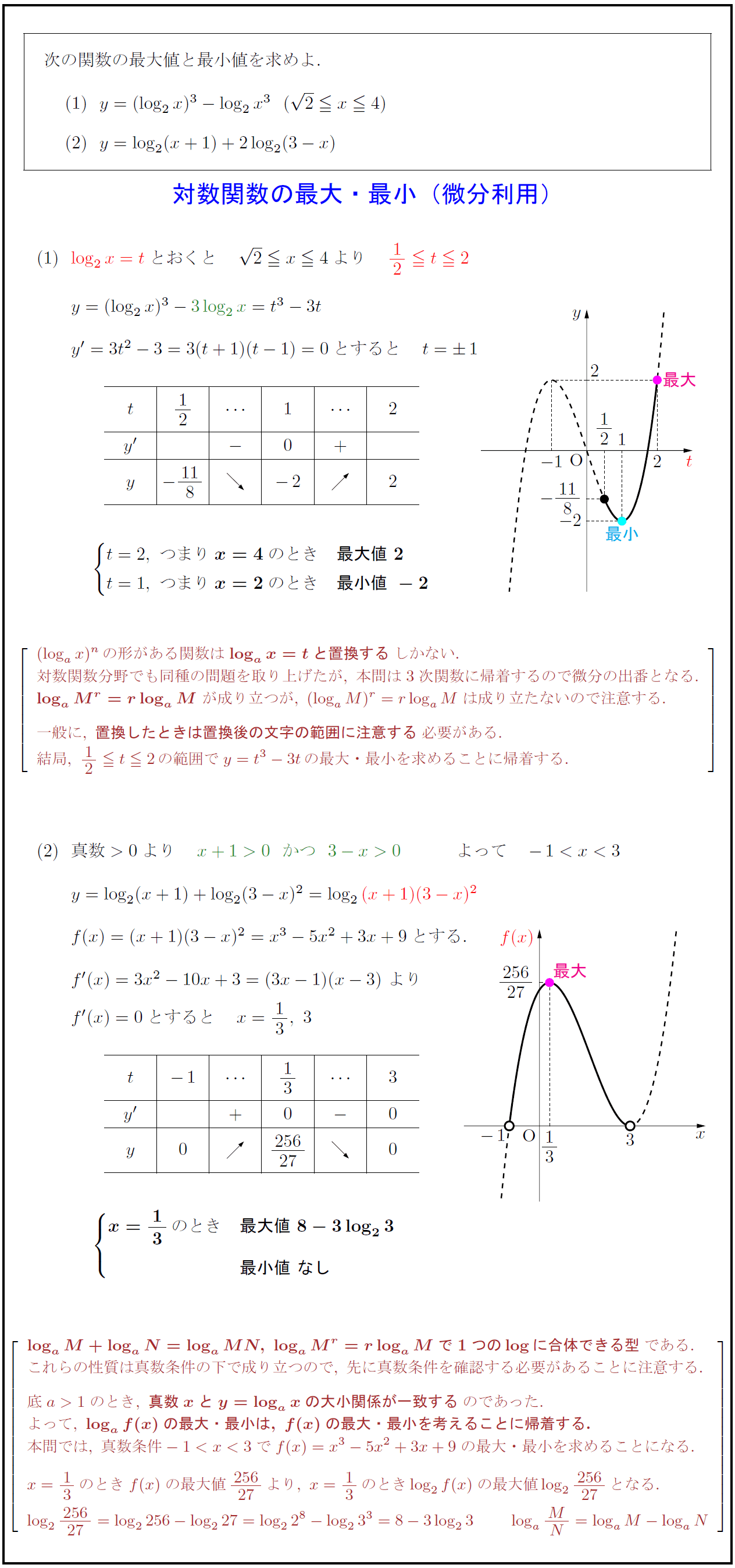
結局,\ 12≦ t≦2\,の範囲でy=t^3-3t\,の最大・最小を求めることに帰着する.
\log_aM+\log_aN=\log_aMN,\ \log_aM^r=r\log_aMで1つの \log に合体できる型}である.
これらの性質は真数条件の下で成り立つので,\ 先に真数条件を確認する必要があることに注意する.
底a>1のとき,\ 真数xとy=\log_ax の大小関係が一致する}のであった.
よって,\ \log_af(x)の最大・最小は,\ f(x)の最大・最小を考えることに帰着する.}
本問では,\ 真数条件でf(x)=x^3-5x^2+3x+9の最大・最小を求めることになる.

