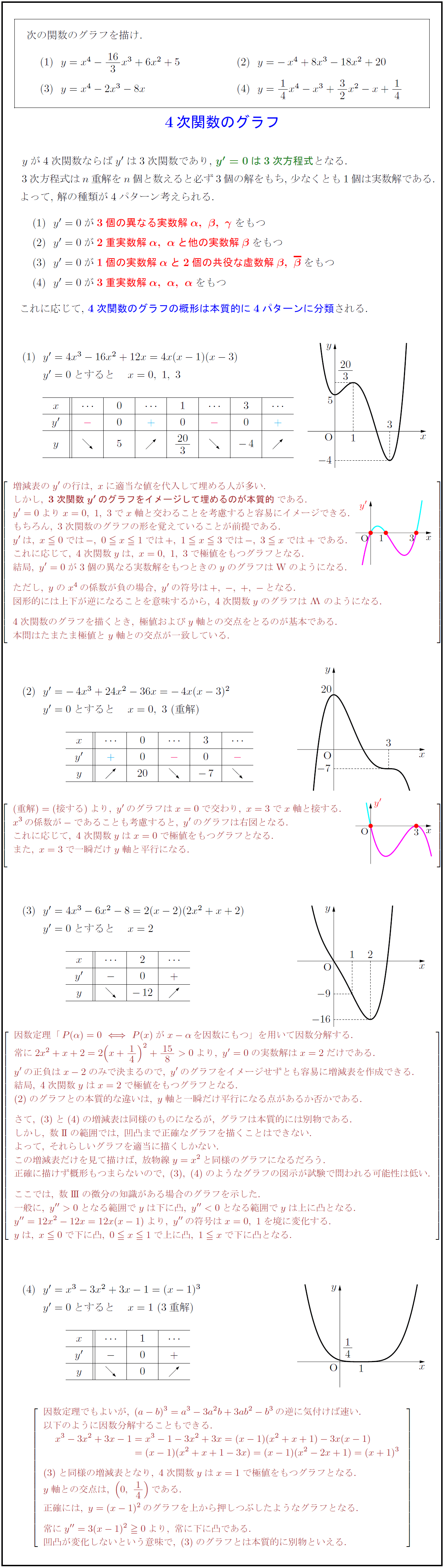
y$が4次関数ならば$y’$は3次関数であり,\{$y’=0}$は3次方程式となる.
3次方程式は$n$重解を$n$個と数えると必ず3個の解をもち,\ 少なくとも1個は実数解である.
よって,\ 解の種類が4パターン考えられる.
(1)\ \ $y’=0$が3個の異なる実数解$α,\ β,\ γ}$をもつ
(2)\ \ $y’=0$が2重実数解$α,\ α}$と他の実数解$β}$をもつ
(3)\ \ $y’=0$が1個の実数解$α}$と2個の共役な虚数解$β,\ β$をもつ
(4)\ \ $y’=0$が3重実数解$α,\ α,\ α}$をもつ
これに応じて,\ 4次関数のグラフの概形は本質的に4パターンに分類される
増減表のy’\,の行は,\ xに適当な値を代入して埋める人が多い.
しかし,\ 3次関数y’\,のグラフをイメージして埋めるのが本質的}である.
y’=0よりx=0,\ 1,\ 3でx軸と交わることを考慮すると容易にイメージできる.
もちろん,\ 3次関数のグラフの形を覚えていることが前提である.
y’\,は,\ x≦0では\,-,\ 0≦ x≦1では\,+,\ 1≦ x≦3では\,-,\ 3≦ xでは+である.
これに応じて,\ 4次関数yは,\ x=0,\ 1,\ 3で極値をもつグラフとなる.
結局,\ y’=0が3個の異なる実数解をもつときのyのグラフはW}のようになる.
ただし,\ yのx^4\,の係数が負の場合,\ y’\,の符号は\,+,\ -,\ +,\ -\,となる.
図形的には上下が逆になることを意味するから,\ 4次関数yのグラフは\ \raisebox{.8zh}{\rotatebox{180}{W\ のようになる.
4次関数のグラフを描くとき,\ 極値およびy軸との交点をとるのが基本である.
本問はたまたま極値とy軸との交点が一致している. \\[-16zh]
(重解)=(接する)より,\ y’\,のグラフはx=0で交わり,\ x=3でx軸と接する.
x^3\,の係数が-であることも考慮すると,\ y’\,のグラフは右図となる.
これに応じて,\ 4次関数yはx=0で極値をもつグラフとなる.
また,\ x=3で一瞬だけy軸と平行になる. \\[-6zh]
因数定理「\,P(α)=0\ ⇔\ P(x)がx-α\,を因数にもつ」を用いて因数分解する.
常より,\ y’=0の実数解はx=2だけである.
y’\,の正負はx-2のみで決まるので,\ y’\,のグラフをイメージせずとも容易に増減表を作成できる.
結局,\ 4次関数yはx=2で極値をもつグラフとなる.
(2)のグラフとの本質的な違いは,\ y軸と一瞬だけ平行になる点があるか否かである.
さて,\ (3)と(4)の増減表は同様のものになるが,\ グラフは本質的には別物である.
しかし,\ 数II}の範囲では,\ 凹凸まで正確なグラフを描くことはできない.
よって,\ それらしいグラフを適当に描くしかない.
この増減表だけを見て描けば,\ 放物線y=x^2\,と同様のグラフになるだろう.
正確に描けず概形もつまらないので,\ (3),\ (4)のようなグラフの図示が試験で問われる可能性は低い.
ここでは,\ 数III}の微分の知識がある場合のグラフを示した.
一般に,\ y”>0となる範囲でyは下に凸,\ y”<0となる範囲でyは上に凸となる.
y''=12x^2-12x=12x(x-1)より,\ y''\,の符号はx=0,\ 1を境に変化する.
yは,\ x≦0で下に凸,\ 0≦ x≦1で上に凸,\ 1≦ xで下に凸となる.
因数定理でもよいが,\ (a-b)^3=a^3-3a^2b+3ab^2-b^3\,の逆に気付けば速い.
以下のように因数分解することもできる.
x^3-3x^2+3x-1=x^3-1-3x^2+3x=(x-1)(x^2+x+1)-3x(x-1)
x^3-3x^2+3x-1}=(x-1)(x^2+x+1-3x)=(x-1)(x^2-2x+1)=(x+1)^3\,
(3)と同様の増減表となり,\ 4次関数yはx=1で極値をもつグラフとなる.
y軸との交点は,\ 0,\ 14である.
正確には,\ y=(x-1)^2\,のグラフを上から押しつぶしたようなグラフとなる.
常にy''=3(x-1)^2≧0より,\ 常に下に凸である.
凹凸が変化しないという意味で,\ (3)のグラフとは本質的に別物といえる.

