「最大値と最小値を求めよ」です。
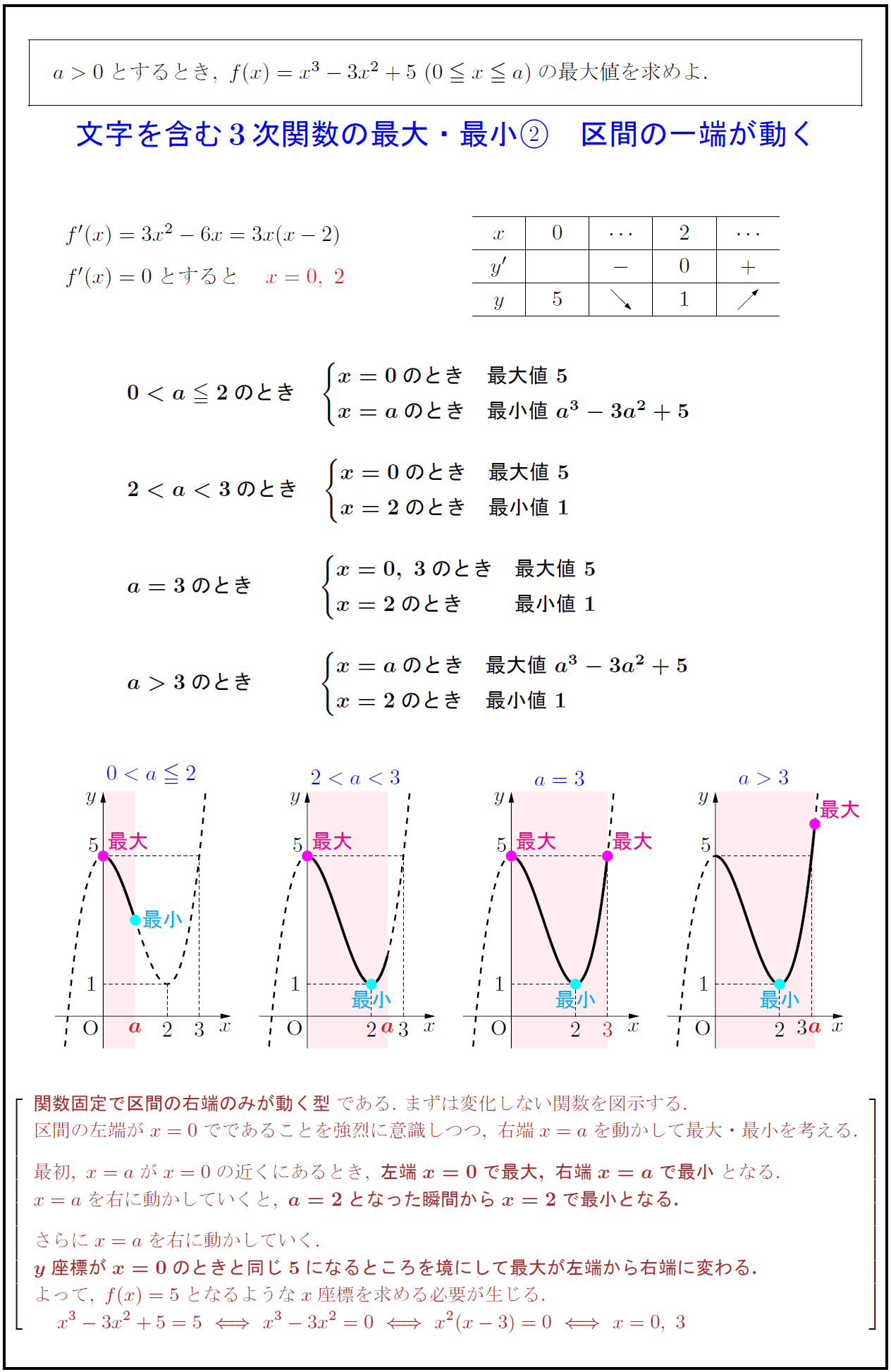
{関数固定で区間の右端のみが動く型}である.\ まずは変化しない関数を図示する.
区間の左端がx=0でであることを強烈に意識しつつ,\ 右端x=aを動かして最大・最小を考える.
最初,\ x=aがx=0の近くにあるとき,\ 左端x=0で最大,\ 右端x=aで最小}となる.
x=aを右に動かしていくと,\ a=2となった瞬間からx=2で最小となる.}
さらにx=aを右に動かしていく.
y座標がx=0のときと同じ5になるところを境にして最大が左端から右端に変わる.}
よって,\ f(x)=5となるようなx座標を求める必要が生じる.

