前項では,\ 増減表を作成してグラフを描く手順を学習した.
しかし,\ {整式の関数の場合,\ 増減表を作成してグラフを描くのは実は本質的ではない.}
本項では,{$f'(x)}$のグラフと$f(x)}$のグラフの関係を学習する.
これにより,{3次関数のグラフの概形が本質的に3通りしかないことがわかる.
f'(x)の正負とf(x)の増減の関係単調に増加}定数(x軸と平行)単調に減少
一般に,\ $f'(x)の正負パターンによってf(x)の概形が決まる.$
よって,\ $f'(x)}$のグラフを元に$f(x)}$\ のグラフの概形を描くことができる.
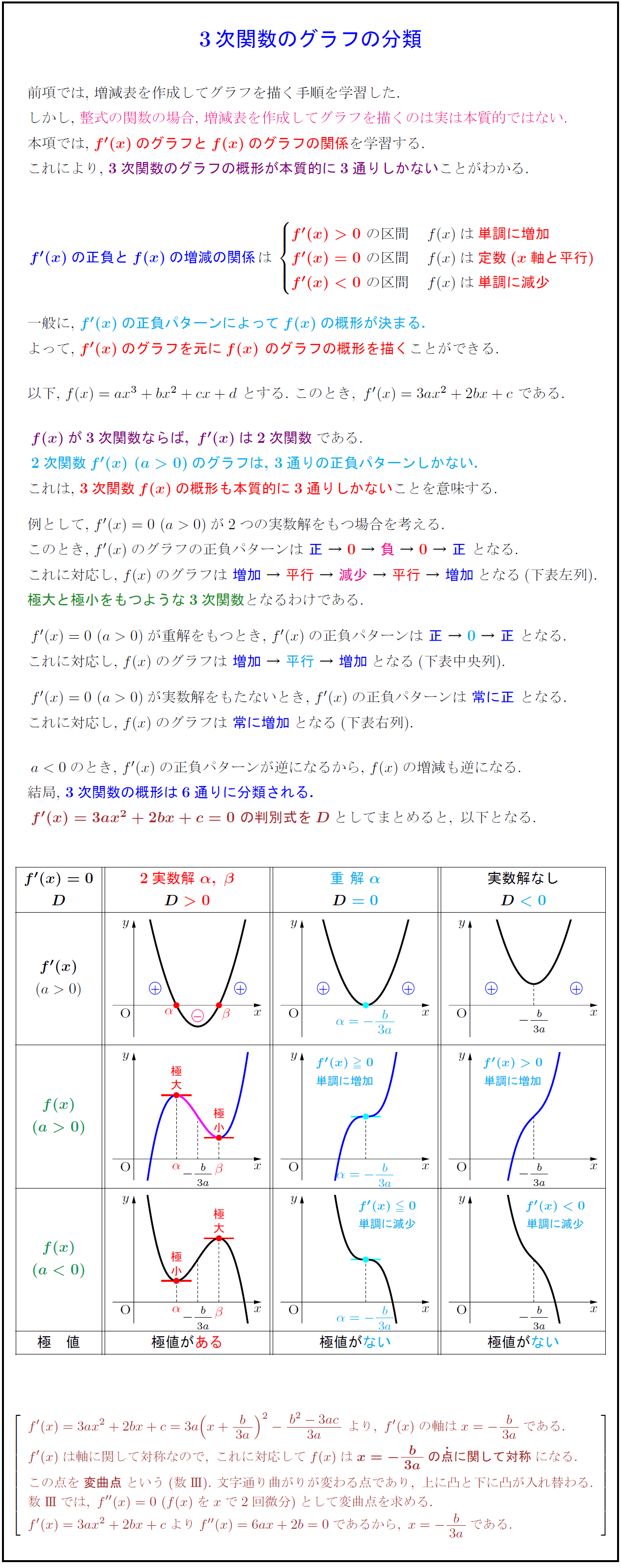
以下,\ $f(x)=ax^3+bx^2+cx+d\ とする.\ このとき,\ f'(x)=3ax^2+2bx+c$\ である.
{f(x)が3次関数ならば,\ f'(x)は2次関数である.$
2次関数$f'(x)\ (a>0)}$のグラフは,\ 3通りの正負パターンしかない.
これは,3次関数$f(x)}$の概形も本質的に3通りしかないことを意味する.
例として,\ $f'(x)=0\ (a>0)$が2つの実数解をもつ場合を考える.
このとき,\ $f'(x)のグラフの正負パターンは極大と極小をもつような3次関数となるわけである.
$f'(x)=0\ (a=0)$が実数解をもたないとき,\ $f'(x)$の正負パターンは\ 常に正\ となる.$
これに対応し,\ $f(x)のグラフは\ 常に増加$となる(下表右列).
$a<0$のとき,\ $f'(x)$の正負パターンが逆になるから,\ $f(x)$の増減も逆になる.
結局,\ 3次関数の概形は6通りに分類される.
f'(x)=3ax^2+2bx+c=0\ の判別式をDとしてまとめると,\ 以下となる.$
f'(x)は軸に関して対称なので,\ これに対応してf(x)はx=-b}{3a}\,の\dot{点}に関して対称}になる.
この点を変曲点}という(数III}).\ 文字通り曲がりが変わる点であり,\ 上に凸と下に凸が入れ替わる.
数III}では,\ f''(x)=0\ (f(x)をxで2回微分)として変曲点を求める.
f'(x)=3ax^2+2bx+cよりf''(x)=6ax+2b=0であるから,\ x=-b}{3a}\,である.

