2曲線\ y=x^3-x,\ y=x^2+a\ が共有点をもち,\ その点で接している.$
そのときの定数$aの値と,\ その接点における共通接線の方程式を求めよ.$ \\
2曲線の共通接線の方程式②(2曲線が接する条件) \\
2曲線$y=f(x),\ y=g(x)}$が同一の接点}($x=p}$)において共通接線をもつ.
このとき,\ 「2曲線が$x=p}$で接する}」}という.
その条件はf(p)=g(p)接点のy座標が一致}) f'(p)=g'(p){接線の傾きが一致})
y=f(x)のx=pにおける接線の方程式は
y=f'(p)(x-p)+f(p) よって y=f'(p)x-pf'(p)+f(p)
y=g(x)のx=pにおける接線の方程式は
y=g'(p)(x-p)+g(p) .2zw}よって y=g'(p)x-pg'(p)+g(p)
この2つの接線の方程式が一致するための条件は,\ 係数比較して
f'(p)=g'(p) かつ -pf'(p)+f(p)=-pg'(p)+g(p)
すなわち f'(p)=g'(p) かつ f(p)=g(p)
この2曲線が$x=p}$で接するための条件は
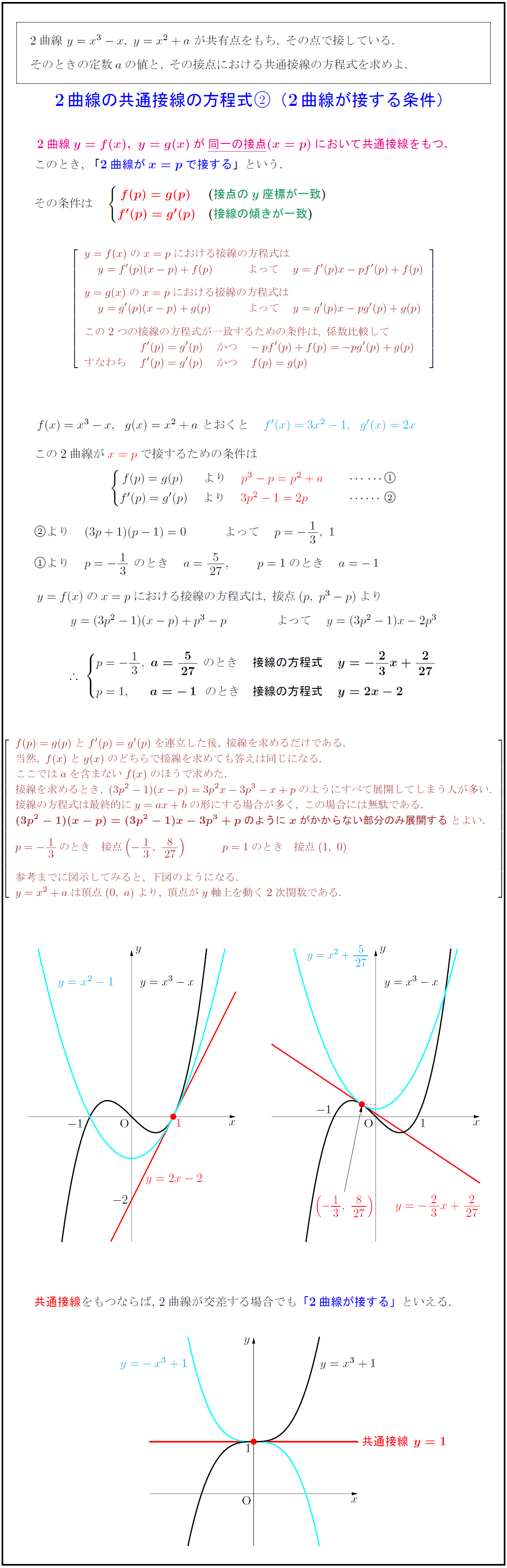
参考までに図示してみると,\ 下図のようになる.
y=x^2+aは頂点(0,\ a)より,\ 頂点がy軸上を動く2次関数である.

