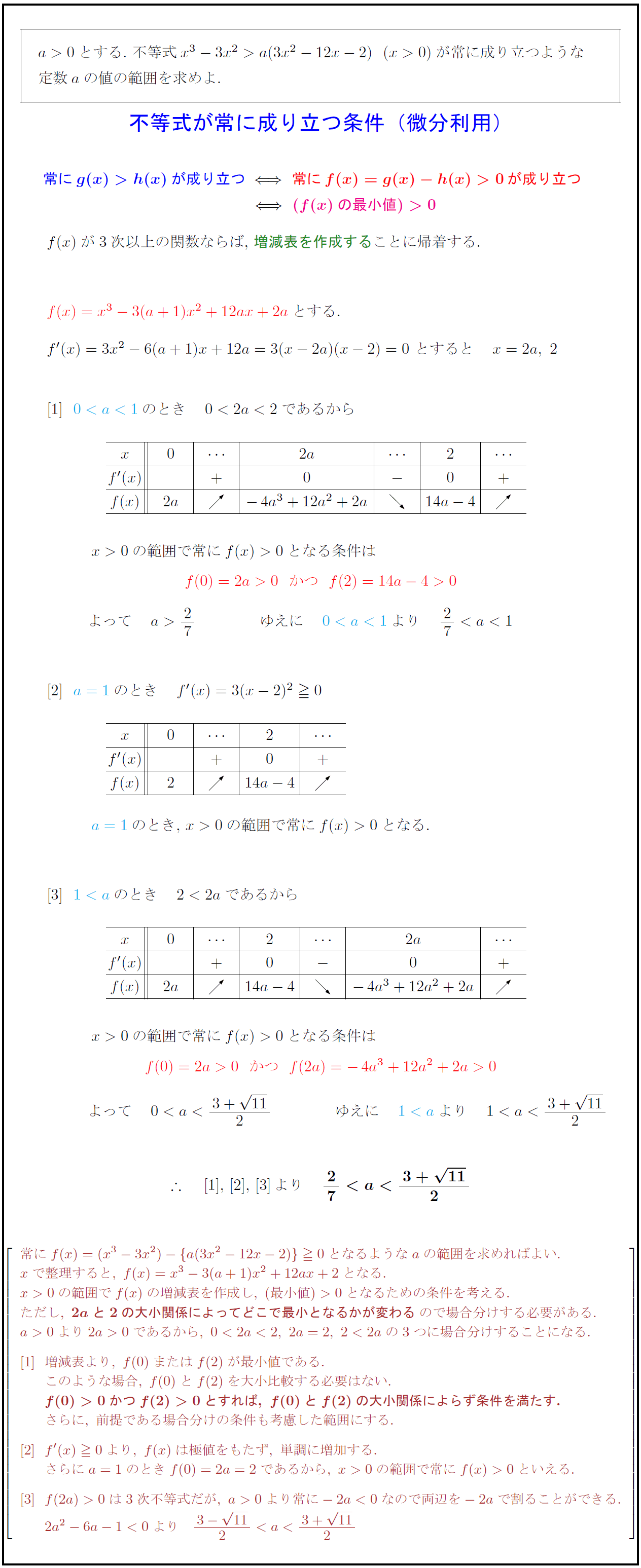
常に$g(x)>h(x)}$が成り立つ$\{常に\,f(x)=g(x)-h(x)>0\,が成り立つ${(f(x)の最小値)>0$
$f(x)$が3次以上の関数ならば,増減表を作成することに帰着する.
常にf(x)=(x^3-3x^2)-\{a(3x^2-12x-2)\}≧0となるようなaの範囲を求めればよい.
xで整理すると,\ f(x)=x^3-3(a+1)x^2+12ax+2となる.
x>0の範囲でf(x)の増減表を作成し,\ (最小値)>0となるための条件を考える.
ただし,\ 2aと2の大小関係によってどこで最小となるかが変わる}ので場合分けする必要がある.
a>0より2a>0であるから,\ 0<2a<2,\ 2a=2,\ 2<2aの3つに場合分けすることになる.
[1]\ \ 増減表より,\ f(0)またはf(2)が最小値である.
\ \ このような場合,\ f(0)とf(2)を大小比較する必要はない.
\ \ f(0)>0かつf(2)>0とすれば,\ f(0)とf(2)の大小関係によらず条件を満たす.}
\ \ さらに,\ 前提である場合分けの条件も考慮した範囲にする.
[2]\ \ f'(x)≧0より,\ f(x)は極値をもたず,\ 単調に増加する.
\ \ さらにa=1のときf(0)=2a=2であるから,\ x>0の範囲で常にf(x)>0といえる.
[3]\ \ f(2a)>0は3次不等式だが,\ a>0より常に-2a<0なので両辺を-2aで割ることができる.

