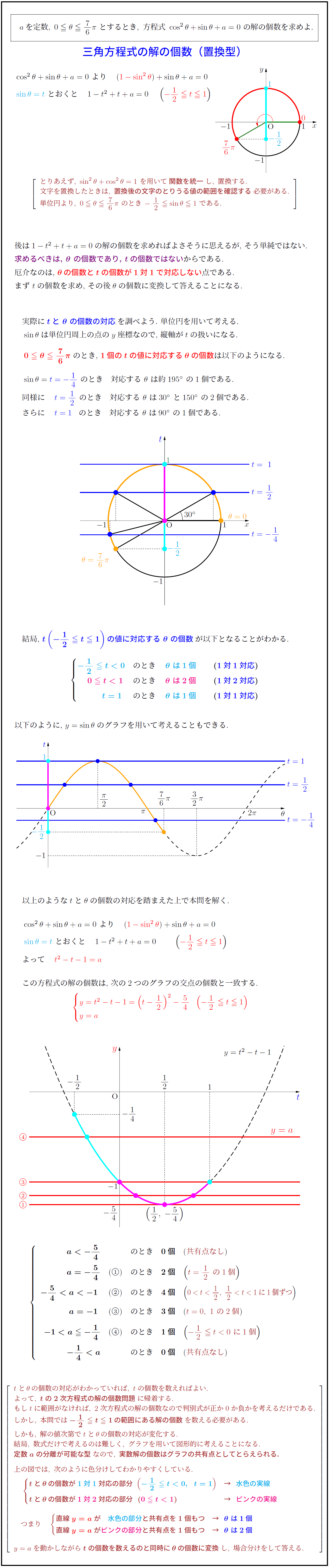
aを定数,\ 0≦θ≦76π\ とするとき,\ 方程式\ \cos^2θ+\sinθ+a=0\ の解の個数を求めよ.${三角方程式の解の個数(置換型)
とりあえず,\ \sin^2θ+\cos^2θ=1\ を用いて関数を統一}し,\ 置換する.
文字を置換したときは,\ 置換後の文字のとりうる値の範囲を確認する}必要がある.
単位円より,\ 0≦θ≦76π\ のとき\,-12≦ \sinθ≦1\ である.
後は$1-t^2+t+a=0$の解の個数を求めればよさそうに思えるが,\ そう単純ではない.
求めるべきは,\ $θ}$\ の個数であり,\ $t}$の個数ではないからである.
厄介なのは,\ $θ}$\,の個数と$t}$の個数が1対1で対応しない点である.
まず $t$の個数を求め,\ その後$θ$の個数に変換して答えることになる.
実際に$tと\ θ\ の個数の対応を調べよう.\ 単位円を用いて考える.$
$\sinθ$は単位円周上の点の$y$座標なので,\ 縦軸が$t$の扱いになる. 1個の$t}$の値に対応する$θ}$の個数は以下のようになる.
$\sinθ=t=-14}\ のとき 対応する\ θ\ は約195°\ の1個である.$
同様に $t=12}\ のとき 対応する\ θ\ は30°\ と150°\ の2個である.$
さらに $t=1}\ \ .2zw}のとき 対応する\ θ\ は90°\ の1個である.$ \\
値に対応する\ θ\ の個数が以下となることがわかる.$
以下のように,\ $y=\sinθ$のグラフを用いて考えることもできる. \
この方程式の解の個数は,\ 次の2つのグラフの交点の個数と一致する.
tと\,θ\,の個数の対応がわかっていれば,\ tの個数を数えればよい.
よって,\ tの2次方程式の解の個数問題}に帰着する.
もしtに範囲がなければ,\ 2次方程式の解の個数なので判別式が正か0か負かを考えるだけである.
しかし,\ 本問では-12≦ t≦1\,の範囲にある解の個数}を数える必要がある.
しかも,\ 解の値次第でtと\,θ\,の個数の対応が変化する.
結局,\ 数式だけで考えるのは難しく,\ グラフを用いて図形的に考えることになる.
定数aの分離が可能な型}なので,\ 実数解の個数はグラフの共有点としてとらえられる.}
上の図では,\ 次のように色分けしてわかりやすくしている.
y=aを動かしながらtの個数を数えるのと同時に\,θ\,の個数に変換}し,\ 場合分けをして答える.

