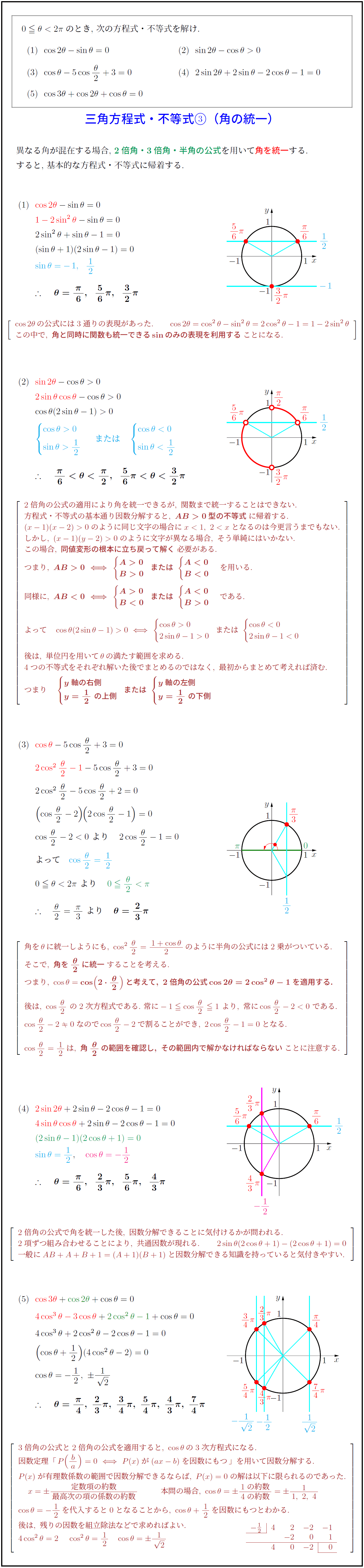
異なる角が混在する場合,\ \textbf{\textcolor[named]{ForestGreen}{2倍角・3倍角・半角の公式}}を用いて\textbf{\textcolor{red}{角を統一}}する. \\[.2zh] すると,\ 基本的な方程式・不等式に帰着する. \cos2\theta\,の公式には3通りの表現があった. この中で,\ \bm{角と同時に関数も統一できる\sin のみの表現を利用する}ことになる. 2倍角の公式の適用により角を統一できるが,\ 関数まで統一することはできない. \\[.2zh] 方程式・不等式の基本通り因数分解すると,\ \bm{AB>0型の不等式}に帰着する. \\[.2zh] (x-1)(x-2)のように同じ文字の場合にとなるのは今更言うまでもない. \\[.2zh] しかし,\ (x-1)(y-2)のように文字が異なる場合,\ そう単純にはいかない. \\[.2zh] この場合,\ \bm{同値変形の根本に立ち戻って解く}必要がある. \\[.2zh] つまり 後は,\ 単位円を用いて\,\theta\,の満たす範囲を求める. \\[.2zh] 4つの不等式をそれぞれ解いた後でまとめるのではなく,\ 最初からまとめて考えれば済む. \\[.5zh] つまり \bm{\begin{cases} y軸の右側 \\[.2zh] y=\bunsuu12\ の上側 \end{cases}\hspace{-.5zw}または\ \begin{cases} y軸の左側 \\[.2zh] y=\bunsuu12\ の下側 角を\,\theta\,に統一しようにも,\ \cos^2\bunsuu{\theta}{2}=\bunsuu{1+\cos\theta}{2}\,のように半角の公式には2乗がついている. \\[.8zh] そこで,\ \bm{角を\,\bunsuu{\theta}{2}\,に統一}することを考える. \\[.8zh] つまり,\ \cos\theta=\bm{\cos\hspace{-.2zw}\left(2\cdot\bunsuu{\theta}{2}\right)と考えて,\ 2倍角の公式\cos2\theta=2\cos^2\theta-1を適用する.} \\\\ 後は,\ \cos\bunsuu{\theta}{2}\ の2次方程式である.\ 常に-1\leqq\cos\bunsuu{\theta}{2}\leqq1\ より,\ 常に\cos\bunsuu{\theta}{2}-2<0\ である. \\[.8zh]
\cos\bunsuu{\theta}{2}-2\neqq0なので\cos\bunsuu{\theta}{2}-2で割ることができ,\ 2\cos\bunsuu{\theta}{2}-1=0となる. \\\\
\cos\bunsuu{\theta}{2}=\bunsuu12\,は,\ \bm{角\,\bunsuu{\theta}{2}\,の範囲を確認し,\ その範囲内で解かなければならない}ことに注意する.
2倍角の公式で角を統一した後,\ 因数分解できることに気付けるかが問われる. \\[.2zh]
2項ずつ組み合わせることにより,\ 共通因数が現れる. 2\sin\theta(2\cos\theta+1)-(2\cos\theta+1)=0 \\[.2zh]
一般にAB+A+B+1=(A+1)(B+1)と因数分解できる知識を持っていると気付きやすい.
3倍角の公式と2倍角の公式を適用すると,\ \cos\theta\,の3次方程式になる. \\[.2zh]
因数定理「\,P\hspace{-.2zw}\left(\bunsuu ba\right)=0\ \Longleftrightarrow\ P(x)が(ax-b)を因数にもつ\,」を用いて因数分解する. \\[.8zh]
P(x)が有理数係数の範囲で因数分解できるならば,\ P(x)=0の解は以下に限られるのであった. \\[.2zh]
x=\pm\bunsuu{定数項の約数}{最高次の項の係数の約数} 本問の場合,\ \cos\theta=\pm\bunsuu{1の約数}{4の約数}=\pm\bunsuu{1}{1,\ 2,\ 4} \\[1zh]
\cos\theta=-\bunsuu12\,を代入すると0となることから,\ \cos\theta+\bunsuu12\,を因数にもつとわかる. \\[.8zh]
後は,\ 残りの因数を組立除法などで求めればよい. \\[.2zh]
