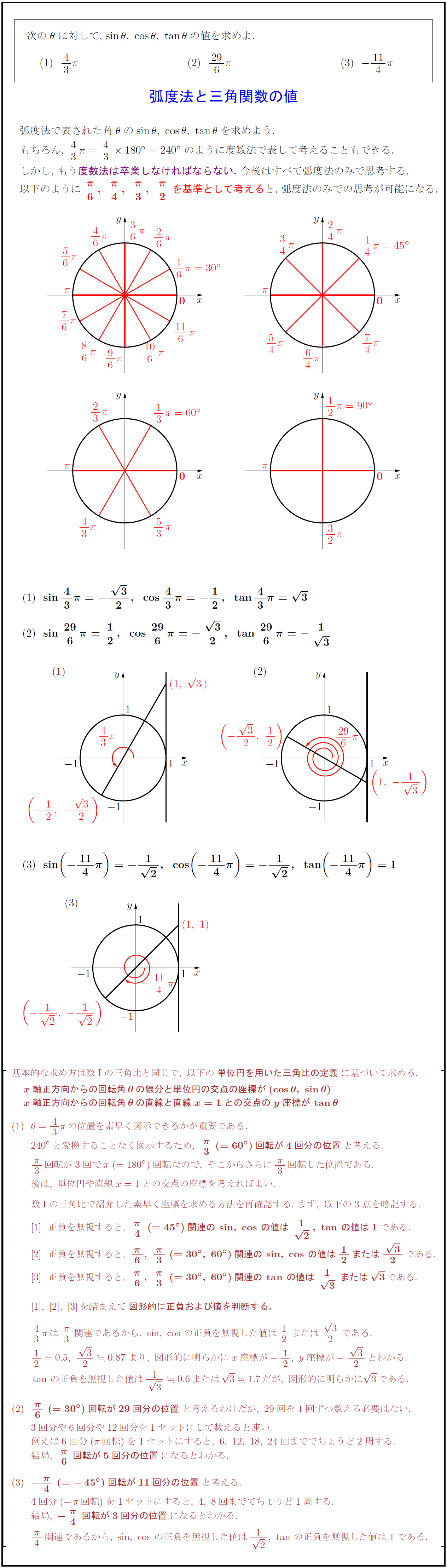
次の$θ$に対して,\ $\sinθ,\ \cosθ,\ \tanθ$の値を求めよ.{弧度法と三角関数の値
弧度法で表された角$θ$の$\sinθ,\ \cosθ,\ \tanθ$を求めよう.
もちろん,\ $43π=43×180°=240°$のように度数法で表して考えることもできる.
しかし,\ もう度数法は卒業しなければならない.\ 今後はすべて弧度法のみで思考する.
以下のように\,$π}{6},\ π}{4},\ π}{3},\ π}{2$を基準として考えると,\ 弧度法のみでの思考が可能になる.
基本的な求め方は数 Iの三角比と同じで,\ 以下の単位円を用いた三角比の定義}に基づいて求める.
x軸正方向からの回転角\,θ\,の線分と単位円の交点の座標が(\cosθ,\ \sinθ)}
x軸正方向からの回転角\,θ\,の直線と直線x=1との交点のy座標が\,\tanθ}
(1)\ \ θ=43π\,の位置を素早く図示できるかが重要である.
\ \ 240°\,と変換することなく図示するため,\ π}{3}\,(=60°)回転が4回分の位置}と考える.
\ \ π}{3}\,回転が3回で\,π\ (=180°)回転なので,\ そこからさらに\,π}{3}\,回転した位置である.
\ \ 後は,\ 単位円や直線x=1との交点の座標を考えればよい.
\ \ 数 Iの三角比で紹介した素早く座標を求める方法を再確認する.\ まず,\ 以下の3点を暗記する.
\ \ [1]\ \ 正負を無視すると,\ π}{4}\ (=45°)関連の\,\sin,\ \cos\,の値は\,1}{√2},\ \tan\,の値は1}である.
\ \ [2]\ \ 正負を無視すると,\ π}{6},\ π}{3}\ (=30°,\ 60°)関連の\,\sin,\ \cos\,の値は\,12\,または\,√3}{2\,である.
\ \ [3]\ \ 正負を無視すると,\ π}{6},\ π}{3}\ (=30°,\ 60°)関連の\,\tan\,の値は\,1}{√3}\,または\,√3}\,である.
\ \ [1],\ [2],\ [3]\,を踏まえて図形的に正負および値を判断する.}
\ \ 43π\,は\,π}{3}\,関連であるから,\ \sin,\ \cos\,の正負を無視した値は\,12\,または\,√3}{2}\,である.
\ \ 12=0.5,\ √3}{2}≒0.87より,\ 図形的に明らかにx座標が-12,\ y座標が-√3}{2}\,とわかる.
\ \ \tan\,の正負を無視した値は\,1}{√3}≒0.6\,または\,√3≒1.7\,だが,\ 図形的に明らかに√3\,である.
(2)\ \ π}{6}\ (=30°)回転が29回分の位置}と考えるわけだが,\ 29回を1回ずつ数える必要はない.
\ \ 3回分や6回分や12回分を1セットにして数えると速い.
\ \ 例えば6回分(π\,回転)を1セットにすると,\ 6,\ 12,\ 18,\ 24回まででちょうど2周する.
\ \ 結局,\ π}{6}\,回転が5回分の位置}になるとわかる.
(3)\ \ -π}{4}\ (=-\,45°)回転が11回分の位置}と考える.
\ \ 4回分(-\,π\,回転)を1セットにすると,\ 4,\ 8回まででちょうど1周する.
\ \ 結局,\ -π}{4}\,回転が3回分の位置}になるとわかる.
\ \ π}{4}\,関連であるから,\ \sin,\ \cos\,の正負を無視した値は\,1}{√2},\ \tan\,の正負を無視した値は1である.

