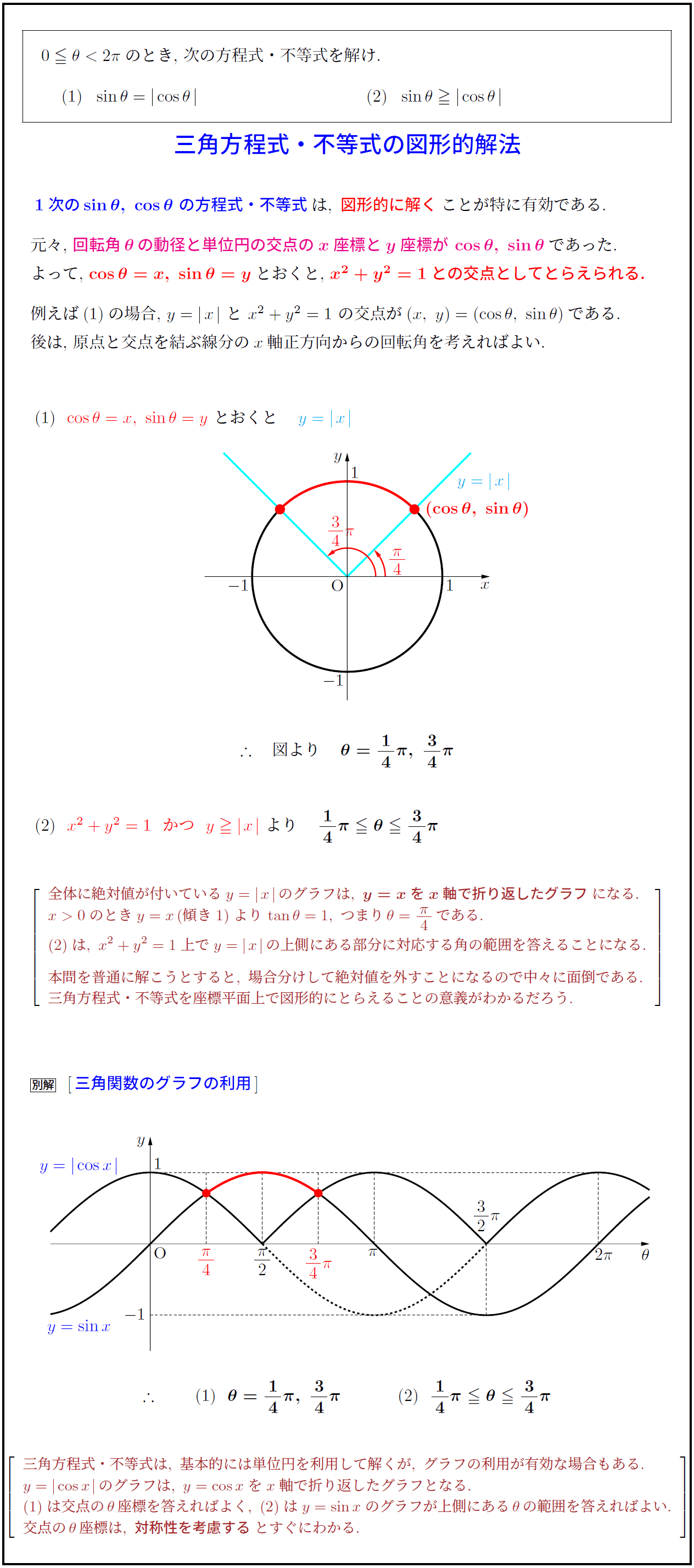
1次の\sinθ,\ \cosθ\ の方程式・不等式は,\ 図形的に解くことが特に有効である.$
元々,\ $回転角\,θ\,の動径と単位円の交点のx座標とy座標が\,\cosθ,\ \sinθであった.$
よって,\ $\cosθ=x,\ \sinθ=y$とおくと,\ $x^2+y^2=1}$との交点としてとらえられる.
例えば(1)の場合,\ $y=x}\ と\ x^2+y^2=1\ の交点が(x,\ y)=(\cosθ,\ \sinθ)である.$
後は,\ 原点と交点を結ぶ線分の$x$軸正方向からの回転角を考えればよい.
(1)\ \ $\cosθ=x,\ \sinθ=y}\ とおくと y=x$
全体に絶対値が付いているy=x}\,のグラフは,\ y=xをx軸で折り返したグラフ}になる.
x>0のときy=x\,(傾き1)より\,\tanθ=1,\ つまり\,θ=π}{4}\,である.
(2)は,\ x^2+y^2=1上でy= x\,の上側にある部分に対応する角の範囲を答えることになる.
本問を普通に解こうとすると,\ 場合分けして絶対値を外すことになるので中々に面倒である.
三角方程式・不等式を座標平面上で図形的にとらえることの意義がわかるだろう.
三角関数のグラフの利用
三角方程式・不等式は,\ 基本的には単位円を利用して解くが,\ グラフの利用が有効な場合もある.
y=\cos x}\,のグラフは,\ y=\cos xをx軸で折り返したグラフとなる.
(1)は交点の\,θ\,座標を答えればよく,\ (2)はy=\sin xのグラフが上側にある\,θ\,の範囲を答えればよい.
交点の\,θ\,座標は,\ 対称性を考慮する}とすぐにわかる.

