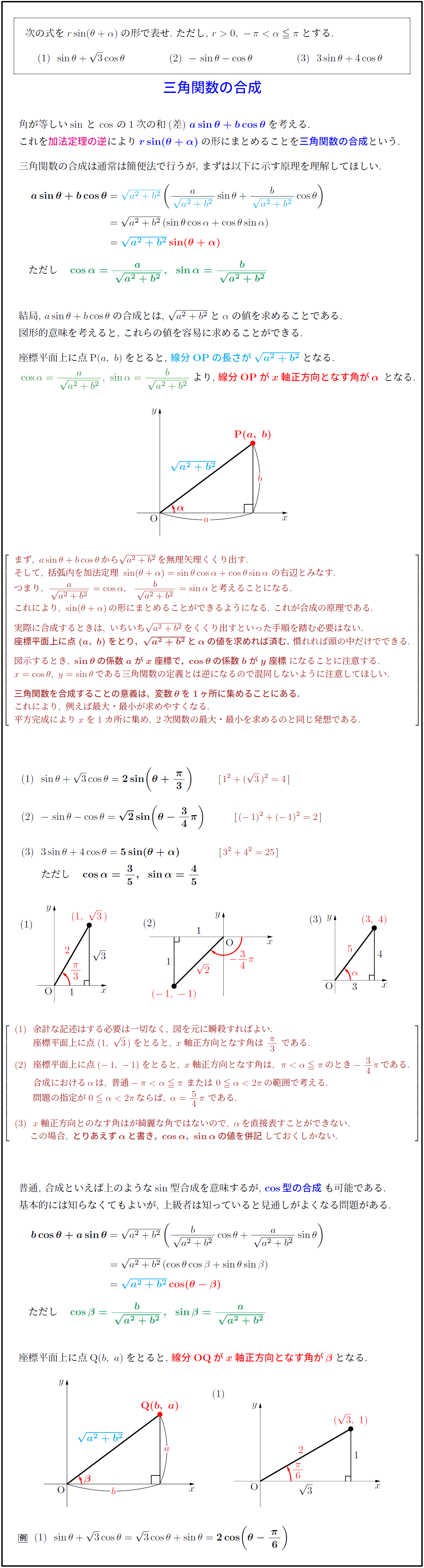
次の式を$r\sin(\theta+\alpha)$の形で表せ.とする. \\[1zh] 角が等しい$\sin\,と\,\cos\,の1次の和(差)\ \bm{\textcolor{blue}{a\sin\theta+b\cos\theta}}$を考える.{加法定理の逆}}により$\bm{\textcolor{blue}{r\sin(\theta+\alpha)}}$の形にまとめることを\textbf{\textcolor{blue}{三角関数の合成}}という. \\[1zh] 三角関数の合成は通常は簡便法で行うが,\ まずは以下に示す原理を理解してほしい. \\[1zh] 結局,\ $a\sin\theta+b\cos\theta$の合成とは,\ $\ruizyoukon{a^2+b^2}$と$\alpha$の値を求めることである. \\[.2zh] 図形的意味を考えると,\ これらの値を容易に求めることができる. \\[1zh] 座標平面上に点P$(a,\ b)$をとると,\ \textbf{\textcolor{cyan}{線分OPの長さ,を無理矢理くくり出す. \\[.2zh] そして,\ 括弧内を加法定理\ \sin(\theta+\alpha)=\sin\theta\cos\alpha+\cos\theta\sin\alpha\ の右辺とみなす. これにより,\ \sin(\theta+\alpha)\,の形にまとめることができるようになる.\ これが合成の原理である. \\[1zh] 実際に合成するときは,\ いちいち\ruizyoukon{a^2+b^2}\,をくくり出すといった手順を踏む必要はない. \\[.2zh] \bm{座標平面上に点(a,\ b)をとり,\ \ruizyoukon{a^2+b^2}\,と\,\alpha\,の値を求めれば済む.}\ 慣れれば頭の中だけでできる. \\[1zh] 図示するとき,\ \bm{\sin\theta\,の係数aがx座標で,\ \cos\theta\,の係数bがy座標}になることに注意する. \\[.2zh] x=\cos\theta,\ y=\sin\theta\,である三角関数の定義とは逆になるので混同しないように注意してほしい. \\[1zh] \bm{三角関数を合成することの意義は,\ 変数\,\theta\,を1ヶ所に集めることにある.} \\[.2zh] これにより,\ 例えば最大・最小が求めやすくなる. \\[.2zh] 平方完成によりxを1カ所に集め,\ 2次関数の最大・最小を求めるのと同じ発想である. (1)\ \ 余計な記述はする必要は一切なく,\ 図を元に瞬殺すればよい. \\[.2zh] \phantom{(1)}\ \ 座標平面上に点(1,\ \ruizyoukon3\,)をとると,\ x軸正方向となす角は\ \bunsuu{\pi}{3}\ である. \\[1zh] (2)\ \ 座標平面上に点(-\,1,\ -\,1)をとると,\ x軸正方向となす角は,\ \,\pi<\alpha\leqq\pi\,のとき-\bunsuu{3}{4}\pi\,である. \\[.8zh] \phantom{(1)}\ \ 合成における\,\alpha\,は,\ 普通または,の範囲で考える. \\[.2zh] \phantom{(1)}\ \ 問題の指定がならば,\ \alpha=\bunsuu54\pi\ である. \\\\ (3)\ \ x軸正方向とのなす角はが綺麗な角ではないので,\ \alpha\,を直接表すことができない. \\[.2zh] \phantom{(1)}\ この場合,\ \bm{とりあえず\,\alpha\,と書き,\ \cos\alpha,\ \sin\alpha\,の値を併記}しておくしかない. 普通,\ 合成といえば上のような$\sin$型合成を意味するが,\ $\bm{\textcolor{blue}{\cos 型の合成}}$も可能である. \\[.2zh] 基本的には知らなくてもよいが,\ 上級者は知っていると見通しがよくなる問題がある. \\[1zh] 座標平面上に点Q$(b,\ a)$をとると,\ $\bm{\textcolor{red}{線分\mathRM{OQ}がx軸正方向となす角が\,\beta}}$となる. \\\\
