3次関数の対称性に関する2つの有名性質を紹介する.
関連問題の見通しがよくなる他,\ 穴埋め問題では強力な裏技となる.
$[1]$\ \ 3次関数は,\ 変曲点に関して点対称である.}(証明は別項)
$[1]$}\ \ 変曲点(数III)とは,\ 文字通り曲がりが変わる点のことである.
$[1]$}\ \ もう少し正確に言えば,\ 上に凸と下に凸が入れ替わる点である.
$[1]$}\ \ 変曲点の$x$座標は,\ $f”(x)=0$\ ($f(x)を2回微分$)によって求めることができる. {変曲点の座標は主要部が横4コ$×}$縦2コの合同な四角形に埋め込まれる.
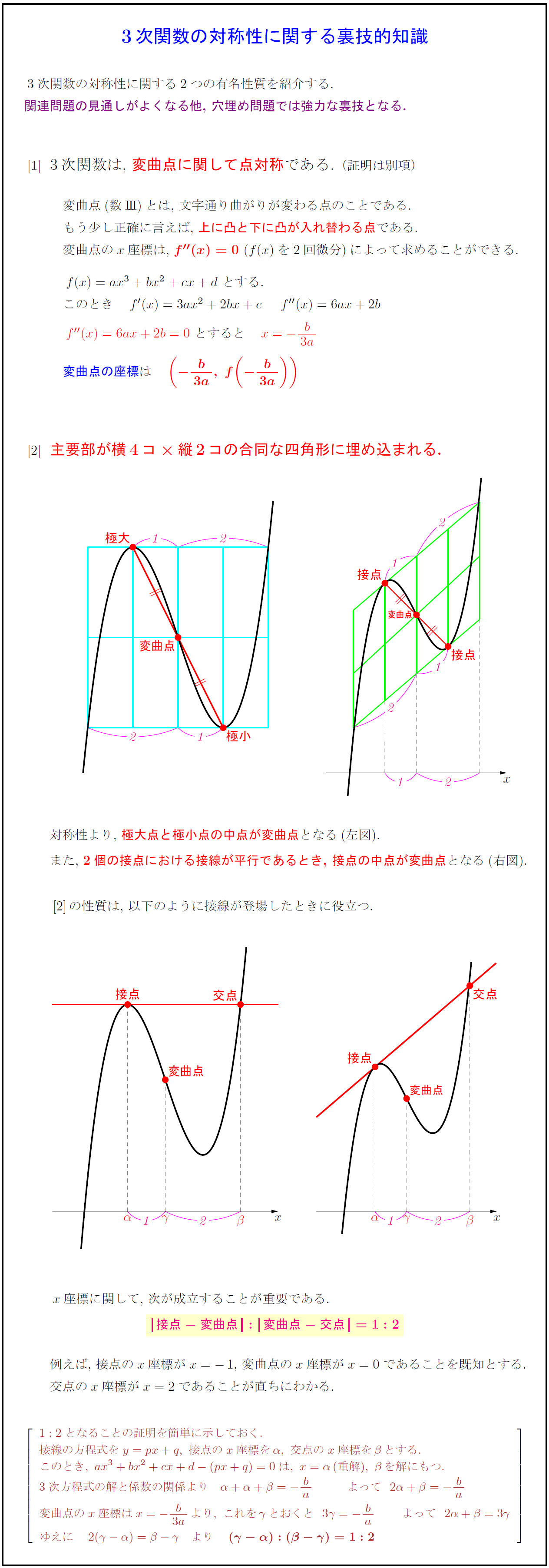
対称性より,\ 極大点と極小点の中点が変曲点となる(左図).
また,\ 2個の接点における接線が平行であるとき,\ 接点の中点が変曲点となる(右図). \\
[2]\,の性質は,\ 以下のように接線が登場したときに役立つ.
$x$座標に関して,\ 次が成立することが重要である. {接点-変曲点}:変曲点-交点}=1:2$
例えば,\ 接点の$x$座標が$x=-\,1$,\ 変曲点の$x$座標が$x=0$であることを既知とする.
交点の$x$座標が$x=2$であることが直ちにわかる.
1:2となることの証明を簡単に示しておく.
接線の方程式をy=px+q,\ 接点のx座標を\,α,\ 交点のx座標を\,β\,とする.
このとき,\ ax^3+bx^2+cx+d-(px+q)=0は,\ x=α\,(重解),\ β\,を解にもつ.
3次方程式の解と係数の関係より α+α+β=- ba よって\ \ 2α+β=- ba
変曲点のx座標は

