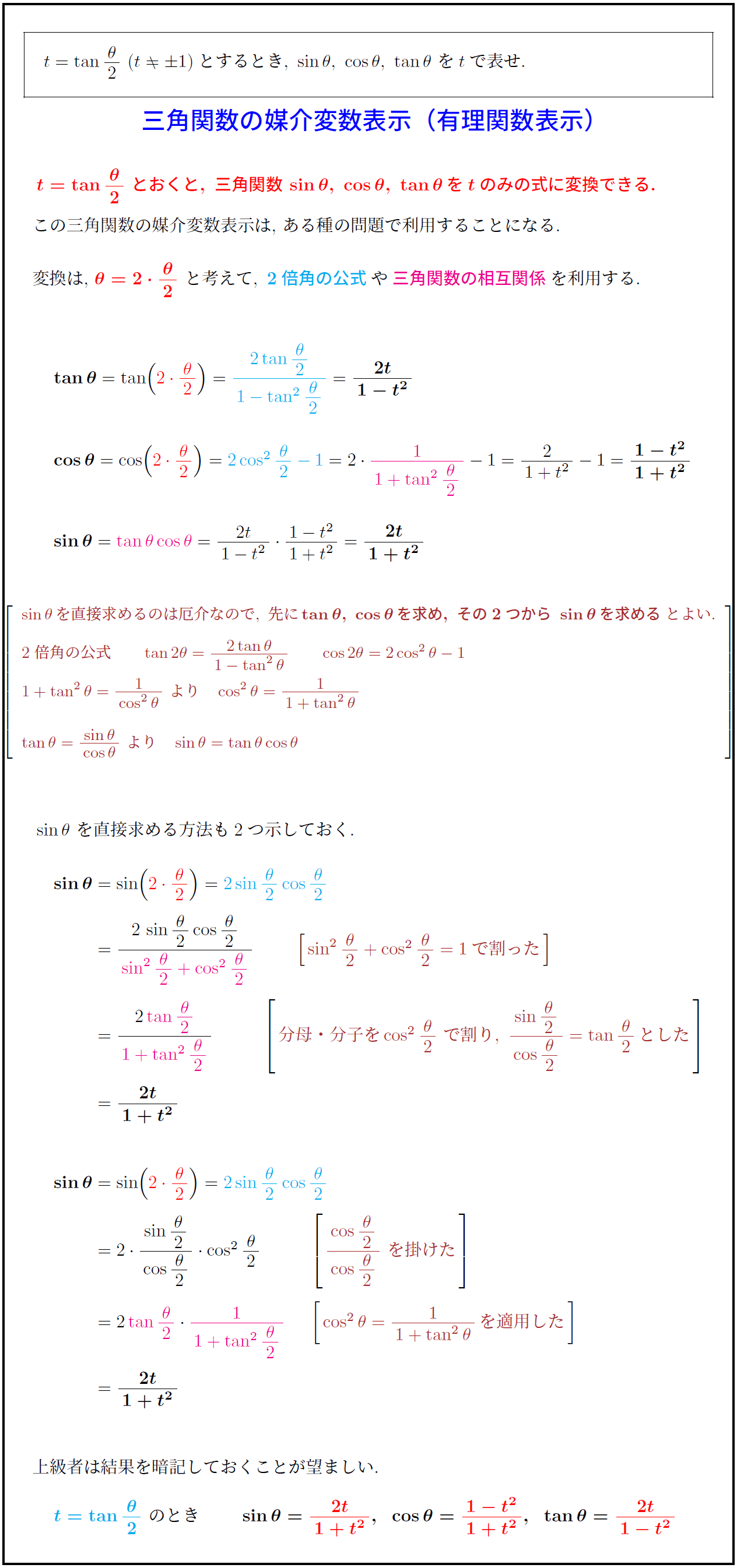
t=\tanθ}{2}\ (t≠±1)とするとき,\ \sinθ,\ \cosθ,\ \tanθ\ をtで表せ.$
三角関数の媒介変数表示(有理関数表示)}$ \\
$t=\tanθ}{2}\ とおくと,\ 三角関数\,\sinθ,\ \cosθ,\ \tanθ\,をtのみの式に変換できる.$
この三角関数の媒介変数表示は,\ ある種の問題で利用することになる.
変換は,\ $θ=2・θ}{2\ と考えて,\ 2倍角の公式や三角関数の相互関係を利用する.$
$\tanθ}=\tan-.2zw}2・θ}{2=2\tanθ}{2{1-\tan^2θ}{2=2t}{1-t^2$ \\
$\cosθ}=\cos-.2zw}2・θ}{2=2\cos^2θ}{2}-1}=2・1}{1+\tan^2θ}{2-1=2}{1+t^2}-1=1-t^2}{1+t^2$ \\
$\sinθ}=\tanθ\cosθ}=2t}{1-t^2}・1-t^2}{1+t^2}=2t}{1+t^2$
$\left[l}
\sinθ\,を直接求めるのは厄介なので,\ 先に\,\tanθ,\ \cosθ\,を求め,\ その2つから\ \sinθ\,を求める}とよい.
2倍角の公式 \tan2θ=2\tanθ}{1-\tan^2θ} \cos2θ=2\cos^2θ-1
1+\tan^2θ=1}{\cos^2θ}\ より \cos^2θ=1}{1+\tan^2θ}
\tanθ=\sinθ}{\cosθ}\ より \sinθ=\tanθ\cosθ
$\sinθ$\ を直接求める方法も2つ示しておく.
$\sinθ}=\sin-.2zw}2・θ}{2=2\sinθ}{2}\cosθ}{2$
$\sinθ=2\,\sinθ}{2}\cosθ}{2{\sin^2θ}{2}+\cos^2θ}{2$ $\left[\,\sin^2θ}{2}+\cos^2θ}{2}=1で割った}\,\right]$
$\sinθ=2\,\tanθ}{2{1+\tan^2θ}{2$ \ \,.2zw}$\left[\,分母・分子を \cos^2θ}{2}\ で割り,\ \sinθ}{2{\cosθ}{2=\tanθ}{2}\,とした}\,\right]$
$\sinθ=2t}{1+t^2$
$\sinθ}=\sin-.2zw}2・θ}{2=2\sinθ}{2}\cosθ}{2$
$\sinθ=2・\sinθ}{2{\cosθ}{2・\cos^2θ}{2}$ \ \ $\left[\,\cosθ}{2{\cosθ}{2\ を掛けた}\,\right]$
$\sinθ=2\,\tanθ}{2・1}{1+\tan^2θ}{2$ $\left[\,\cos^2θ=1}{1+\tan^2θ}\,を適用した}\,\right]$
$\sinθ=2t}{1+t^2$
上級者は結果を暗記しておくことが望ましい.
$t=\tanθ}{2\ のとき$ $\sinθ=2t}{1+t^2,\ \ \cosθ=1-t^2}{1+t^2,\ \ \tanθ=2t}{1-t^2$

