2次方程式ならば,\ 実数解の個数は判別式で容易に調べることができる.
しかし,\ 3次方程式の判別式は高校では学習しないので,\ グラフを用いて図形的に考える}ことになる.
方程式の実数解の個数は,\ 図形的には共有点の個数}である.
本問のように,\ 定数が完全に分離できる場合,\ 3次関数と直線の共有点の個数に帰着}する.
2x^3-3x^2-12x=-\,k\ としてもよいが,\ 直線\ y=-\,k\ を考えることになり,\ 正負がまぎらわしい.
よって,\ +\,kとして分離するべきである.
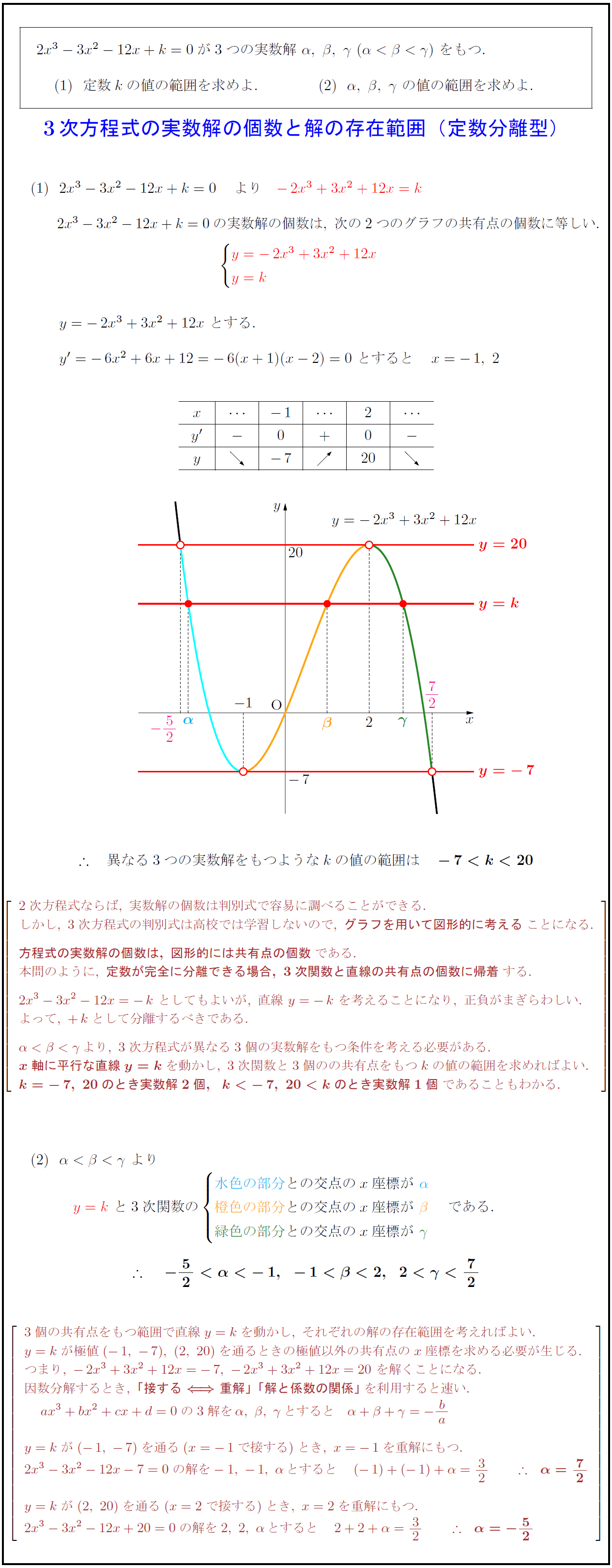
α<β<γ\,より,\ 3次方程式が異なる3個の実数解をもつ条件を考える必要がある.
x軸に平行な直線y=k}を動かし,\ 3次関数と3個のの共有点をもつkの値の範囲を求めればよい.
k=-\,7,\ 20のとき実数解2個,\ \ k<-\,7,\ 20

