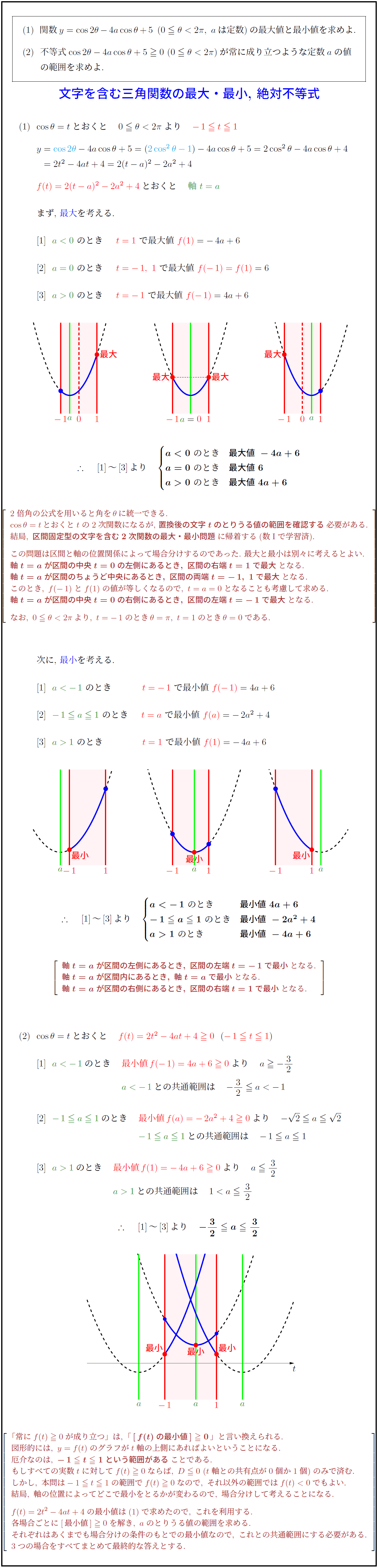
関数$y=\cos2θ-4a\cosθ+5\ \,(0≦ θ<2π,\ aは定数)$の最大値と最小値を求めよ.
(2)\ \ 不等式$\cos2θ-4a\cosθ+5≧0\ (0≦ θ<2π)$が常に成り立つような定数$a$の値
\ \ の範囲を求めよ.{文字を含む三角関数の最大・最小,\ 絶対不等式
2倍角の公式を用いると角を\,θ\,に統一できる.
\cosθ=t\,とおくとtの2次関数になるが,\,置換後の文字tのとりうる値の範囲を確認する}必要がある.
結局,\ 区間固定型の文字を含む2次関数の最大・最小問題}に帰着する(数 Iで学習済).
この問題は区間と軸の位置関係によって場合分けするのであった.\ 最大と最小は別々に考えるとよい.
軸t=aが区間の中央t=0の左側にあるとき,\ 区間の右端t=1で最大}となる.
軸t=aが区間のちょうど中央にあるとき,\ 区間の両端t=-\,1,\ 1で最大}となる.
このとき,\ f(-\,1)とf(1)の値が等しくなるので,\ t=a=0となることも考慮して求める.
軸t=aが区間の中央t=0の右側にあるとき,\ 区間の左端t=-\,1で最大}となる.
なお,\ 0≦θ<2π\,より,\ t=-\,1のとき\,θ=π,\ t=1のとき\,θ=0である.
軸t=aが区間の左側にあるとき,\ 区間の左端t=-\,1で最小}となる.
軸t=aが区間内にあるとき,\ 軸t=aで最小}となる.
軸t=aが区間の右側にあるとき,\ 区間の右端t=1で最小}となる.
「常にf(t)≧0が成り立つ」は,\ 「\,[\,f(t)の最小値\,]≧0}\,」と言い換えられる.
図形的には,\ y=f(t)のグラフがt軸の上側にあればよいということになる.
厄介なのは,\ -\,1≦ t≦1という範囲がある}ことである.
もしすべての実数tに対してf(t)≧0ならば,\ D≦0\ (t軸との共有点が0個か1個)のみで済む.
しかし,\ 本問は-1≦ t≦1の範囲でf(t)≧0なので,\ それ以外の範囲ではf(t)<0でもよい.
結局,\ 軸の位置によってどこで最小をとるかが変わるので,\ 場合分けして考えることになる.
f(t)=2t^2-4at+4の最小値は(1)で求めたので,\ これを利用する.
各場合ごとに[\,最小値\,]≧0を解き,\ aのとりうる値の範囲を求める.
それぞれはあくまでも場合分けの条件のもとでの最小値なので,\ これとの共通範囲にする必要がある.
3つの場合をすべてまとめて最終的な答えとする.

