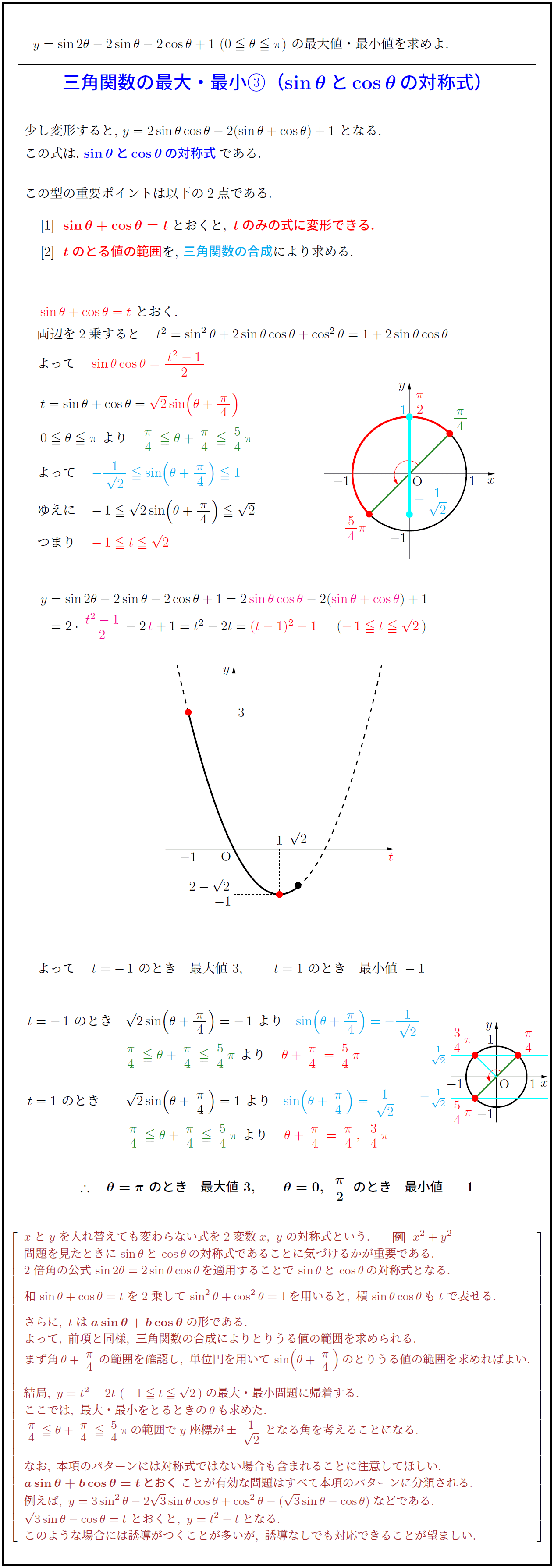
y=\sin2θ-2\sinθ-2\cosθ+1\ (0≦θ≦π)\ の最大値・最小値を求めよ.$ 三角関数の最大・最小③($\sinθ\,と\cosθ\,の対称式}$) \\
少し変形すると,\ $y=2\sinθ\cosθ-2(\sinθ+\cosθ)+1$\ となる.
この式は,\ $\sinθ\,と\cosθ\,の対称式$である.
この型の重要ポイントは以下の2点である.
$[1]$\ \ $\sin{θ}+\cos{θ}=tとおくと,\ tのみの式に変形できる.$
$[2]$\ \ $t}$のとる値の範囲を,\ 三角関数の合成により求める.
$\sin{θ}+\cos{θ}=t}\ とおく.$
両辺を2乗すると
xとyを入れ替えても変わらない式を2変数x,\ yの対称式という. \rei\ \ x^2+y^2
問題を見たときに\,\sinθ\,と\,\cosθ\,の対称式であることに気づけるかが重要である.
2倍角の公式\,\sin2θ=2\sinθ\cosθ\,を適用することで\,\sinθ\,と\,\cosθ\,の対称式となる.
和\,\sinθ+\cosθ=tを2乗して\,\sin^2θ+\cos^2θ=1\,を用いると,\ 積\,\sinθ\cosθ\,もtで表せる.
さらに,\ tはa\sinθ+b\cosθ}の形である.
よって,\ 前項と同様,\ 三角関数の合成によりとりうる値の範囲を求められる.
まず角\,θ+π}{4}\,の範囲を確認し,\ 単位円を用いて\,\sin-.2zw}θ+π}{4}のとりうる値の範囲を求めればよい.
結局,\ y=t^2-2t\ (-\,1≦ t≦√2\,)の最大・最小問題に帰着する.
ここでは,\ 最大・最小をとるときの\,θ\,も求めた.
π}{4}≦θ+π}{4}≦54π\,の範囲でy座標が±1}{√2}\,となる角を考えることになる.
本項のパターンには対称式ではない場合も含まれるが,\ a\sinθ+b\cosθ=t\,とおくのは同じである.
例えば,\ y=2\sinθ\cosθ-(√3\sinθ-\cosθ)ならば,\ √3\sinθ-\cosθ=t\ とおけばよい.

