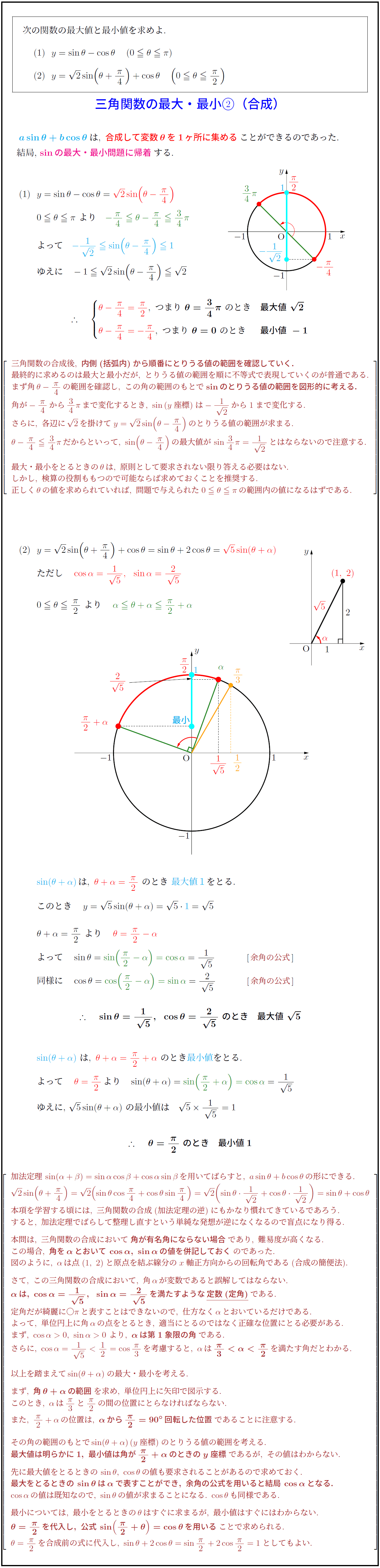
次の関数の最大値と最小値を求めよ. 三角関数の最大・最小②(合成) \\
$a\sinθ+b\cosθは,\ 合成して変数\,θ\,を1ヶ所に集める$ことができるのであった.
結局,\ $\sin の最大・最小問題に帰着する.$
三角関数の合成後,\ 内側(括弧内)から順番にとりうる値の範囲を確認していく.}
最終的に求めるのは最大と最小だが,\ とりうる値の範囲を順に不等式で表現していくのが普通である.
まず角\,θ-π}{4}\,の範囲を確認し,\ この角の範囲のもとで\sin のとりうる値の範囲を図形的に考える.}
角が-π}{4}\,から\,34π\,まで変化するとき,\ \sin\,(y座標)は-1}{√2}\,から1まで変化する.
さらに,\ 各辺に\,√2\,を掛けてy=√2\sin-.2zw}θ-π}{4}のとりうる値の範囲が求まる.
θ-π}{4}≦34π\,だからといって,\ \sin-.2zw}θ-π}{4}の最大値が\,\sin34π=1}{√2}\,とはならないので注意する.
最大・最小をとるときの\,θ\,は,\ 原則として要求されない限り答える必要はない.
しかし,\ 検算の役割ももつので可能ならば求めておくことを推奨する.
正しく\,θ\,の値を求められていれば,\ 問題で与えられた0≦θ≦π\,の範囲内の値になるはずである.
加法定理\,\sin(α+β)=\sinα\cosβ+\cosα\sinβ\,を用いてばらすと,\ a\sinθ+b\cosθ\,の形にできる.
本項を学習する頃には,\ 三角関数の合成(加法定理の逆)にもかなり慣れてきているであろう.
すると,\ 加法定理でばらして整理し直すという単純な発想が逆になくなるので盲点になり得る.
本問は,\ 三角関数の合成において角が有名角にならない場合}であり,\ 難易度が高くなる.
この場合,\ 角を\,α\,とおいて\,\cosα,\ \sinα\,の値を併記しておく}のであった.
図のように,\ α\,は点(1,\ 2)と原点を結ぶ線分のx軸正方向からの回転角である(合成の簡便法).
さて,\ この三角関数の合成において,\ 角\,α\,が変数であると誤解してはならない.
α\,は,\ \cosα=1}{√5},\ \ \sinα=2}{√5}\,を満たすような\,定数(定角)である.
定角だが綺麗に○π\,と表すことはできないので,\ 仕方なく\,α\,とおいているだけである.
よって,\ 単位円上に角\,α\,の点をとるとき,\ 適当にとるのではなく正確な位置にとる必要がある.
まず,\ \cosα>0,\ \sinα>0\ より,\ α\,は第1象限の角}である.
さらに,\ \cosα=1}{√5}<12=\cosπ}{3}\,を考慮すると,\ α\,は\,π}{3}<α<π}{2\,を満たす角だとわかる.
以上を踏まえて\sin(θ+α)の最大・最小を考える.
まず,\ 角\,θ+α\,の範囲}を求め,\ 単位円上に矢印で図示する.
このとき,\ α\,は\,π}{3}\,と\,π}{2}\,の間の位置にとらなければならない.
また,\ π}{2}+α\,の位置は,\ α\,から\,π}{2}=90°\,回転した位置}であることに注意する.
その角の範囲のもとで\sin(θ+α)\,(y座標)のとりうる値の範囲を考える.
最大値は明らかに1,\ 最小値は角が\,π}{2}+α\,のときのy座標}であるが,\ その値はわからない.
先に最大値をとるときの\,\sinθ,\ \cosθ\,の値も要求されることがあるので求めておく.
最大をとるときの\,\sinθ\,は\,α\,で表すことができ,\ 余角の公式を用いると結局\,\cosα\,となる.}
\cosα\,の値は既知なので,\ \sinθ\,の値が求まることになる.\ \cosθ\,も同様である.
最小については,\ 最小をとるときの\,θ\,はすぐに求まるが,\ 最小値はすぐにはわからない.
θ=π}{2}\,を代入し,\ 公式\,\sin-.2zw}π}{2}+θ=\cosθ\,を用いる}ことで求められる.
θ=π}{2}\,を合成前の式に代入し,\ \sinθ+2\cosθ=\sinπ}{2}+2\cosπ}{2}=1としてもよい.

