4次関数$y=x^4-2x^3-11x^2$と異なる2点で接する直線の方程式を求めよ. \\
4次関数の二重接線の方程式 \\
求める直線の方程式を$y=mx+n$とおく.
この直線と$y=x^4-2x^3-11x^2$との接点の$x$座標を$α,\ β$とする.
このとき,\ 恒等式$x^4-2x^3-11x^2-(mx+n)=(x-α)^2(x-β)^2}\ ・・・\,\maru{ A}$\ が成立する.
ここで,\ $α,\ β$は$t^2-t-6=0$の2解である.
これを解くと $(t+2)(t-3)=0$より $t=-\,2,\ 3$
よって,\ $y=x^4-2x^3-11x^2$と$x=-\,2,\ 3$で接するような直線が存在する.}
ゆえに,\ ③,\ ④より $m=-\,12,\ n=-\,36$
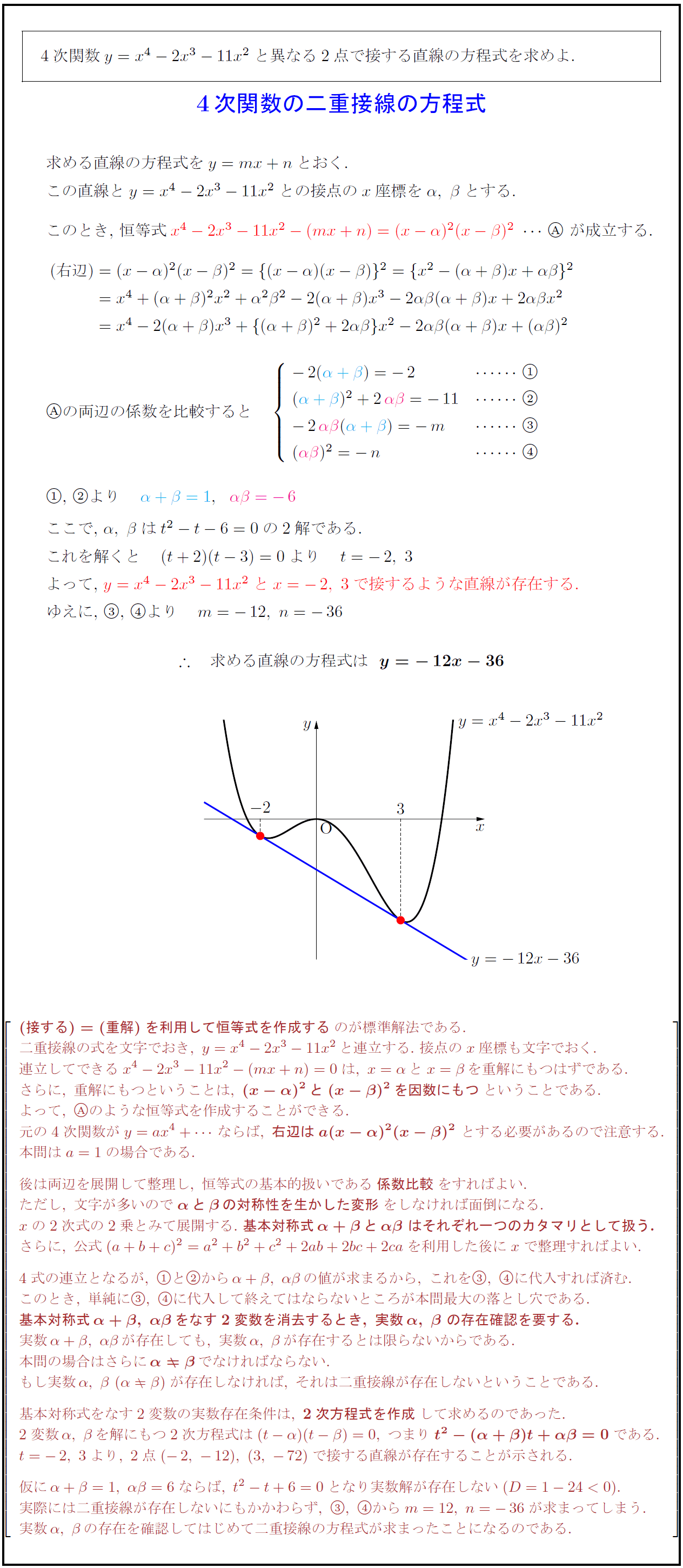
∴$ 求める直線の方程式は\ \ $y=-\,12x-36}$}
(接する)=(重解)を利用して恒等式を作成する}のが標準解法である.
二重接線の式を文字でおき,\ y=x^4-2x^3-11x^2\,と連立する.\ 接点のx座標も文字でおく.
連立してできるx^4-2x^3-11x^2-(mx+n)=0は,\ x=α\,とx=β\,を重解にもつはずである.
さらに,\ 重解にもつということは,\ (x-α)^2\,と(x-β)^2\,を因数にもつ}ということである.
よって,\ \maru{ A}のような恒等式を作成することができる.
元の4次関数がy=ax^4+・・・\,ならば,\ 右辺はa(x-α)^2(x-β)^2}\ とする必要があるので注意する.
本問はa=1の場合である.
後は両辺を展開して整理し,\ 恒等式の基本的扱いである係数比較}をすればよい.
ただし,\ 文字が多いのでα\,と\,β\,の対称性を生かした変形}をしなければ面倒になる.
xの2次式の2乗とみて展開する.\ 基本対称式\,α+β\,と\,αβ\ はそれぞれ一つのカタマリとして扱う.}
さらに,\ 公式(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2caを利用した後にxで整理すればよい.
4式の連立となるが,\ ①と②から\,α+β,\ αβ\,の値が求まるから,\ これを③,\ ④に代入すれば済む.
このとき,\ 単純に③,\ ④に代入して終えてはならないところが本問最大の落とし穴である.
基本対称式\,α+β,\ αβ\,をなす2変数を消去するとき,\ 実数\,α,\ β\ の存在確認を要する.}
実数\,α+β,\ αβ\,が存在しても,\ 実数\,α,\ β\,が存在するとは限らないからである.
本問の場合はさらに\,α≠β}\,でなければならない.
もし実数\,α,\ β\ (α≠β)が存在しなければ,\ それは二重接線が存在しないということである.
基本対称式をなす2変数の実数存在条件は,\ 2次方程式を作成}して求めるのであった.
2変数\,α,\ β\,を解にもつ2次方程式は(t-α)(t-β)=0,\ つまりt^2-(α+β)t+αβ=0}である.
t=-\,2,\ 3より,\ 2点(-\,2,\ -\,12),\ (3,\ -\,72)で接する直線が存在することが示される.
仮に\,α+β=1,\ αβ=6ならば,\ t^2-t+6=0となり実数解が存在しない(D=1-24<0).
実際には二重接線が存在しないにもかかわらず,\ ③,\ ④からm=12,\ n=-\,36が求まってしまう.
実数\,α,\ β\,の存在を確認してはじめて二重接線の方程式が求まったことになるのである.

