3次関数に引ける接線の本数問題の基本方針については前項で説明した.
接線が点$(a,\ b)$を通るように立式すると,\ 実数解の個数問題に帰着するのであった.
ただし,\ 前項とは異なり,\ 定数が分離できない型の実数解の個数問題に帰着する.
定数が分離できない場合,\ 極値の積を利用するのであった.
接点を\ P$(t,\ t^3-t)$\ とおく.
$y’=3x^2-1$より,\ 点Pにおける接線の方程式は
$y=(3t^2-1)(x-t)+(t^3-t) よって y=(3t^2-1)x-2t^3$
この直線が$点(a,\ b)を通るから b=(3t^2-1)a-2t^3$
}{3次関数では接点の個数と接線の本数が一致する.
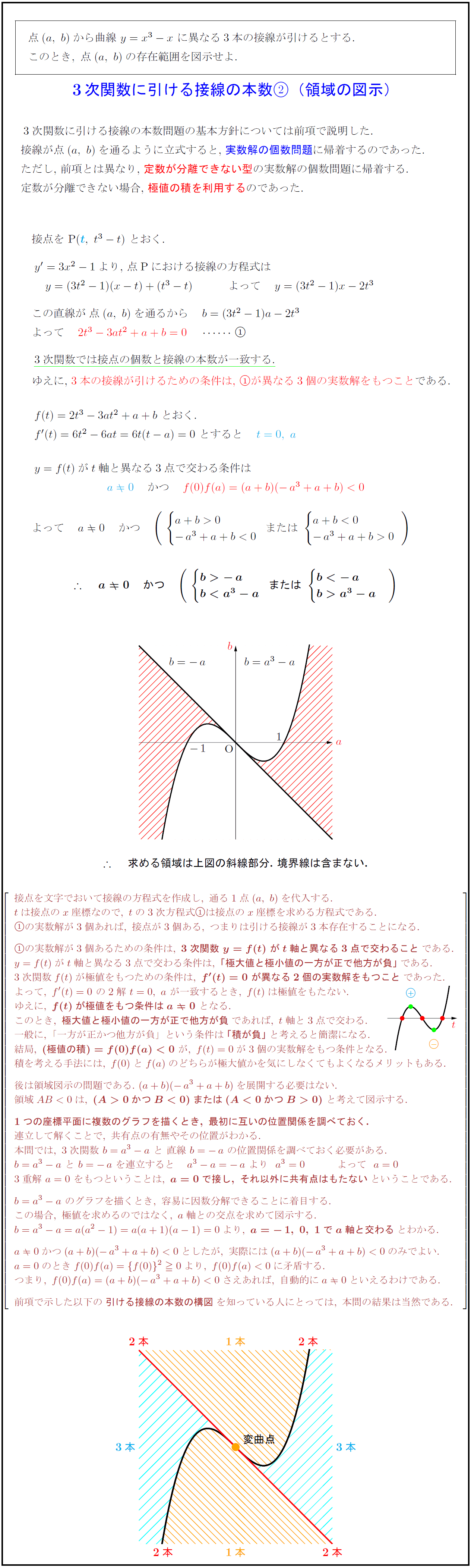
ゆえに,\ 3本の接線が引けるための条件は,\ ①が異なる3個の実数解をもつこと}である{求める領域は上図の斜線部分.\ 境界線は含まない.}$
接点を文字でおいて接線の方程式を作成し,\ 通る1点(a,\ b)を代入する.
tは接点のx座標なので,\ tの3次方程式①は接点のx座標を求める方程式である.
①の実数解が3個あれば,\ 接点が3個ある,\ つまりは引ける接線が3本存在することになる.
①の実数解が3個あるための条件は,\ 3次関数\ y=f(t)\ がt軸と異なる3点で交わること}である.
y=f(t)がt軸と異なる3点で交わる条件は,\ 「極大値と極小値の一方が正で他方が負」}である.
3次関数f(t)が極値をもつための条件は,\ f'(t)=0\ が異なる2個の実数解をもつこと}であった.
よって,\ f'(t)=0\ の2解\ t=0,\ a\ が一致するとき,\ f(t)は極値をもたない.
ゆえに,\ f(t)が極値をもつ条件はa≠0}\ となる.
このとき,\ 極大値と極小値の一方が正で他方が負}であれば,\ t軸と3点で交わる.
一般に,\ 「一方が正かつ他方が負」という条件は「積が負」}と考えると簡潔になる.
結局,\ (極値の積)=f(0)f(a)<0}\ が,\ f(t)=0が3個の実数解をもつ条件となる.
積を考える手法には,\ f(0)とf(a)のどちらが極大値かを気にしなくてもよくなるメリットもある. \\
後は領域図示の問題である.\ (a+b)(-\,a^3+a+b)を展開する必要はない.
領域AB<0は,\ (A>0かつB<0)または(A<0かつB>0)}\ と考えて図示する.
1つの座標平面に複数のグラフを描くとき,\ 最初に互いの位置関係を調べておく.}
連立して解くことで,\ 共有点の有無やその位置がわかる.
本問では,\ 3次関数\ b=a^3-a\ と\ 直線\ b=-\,a\ の位置関係を調べておく必要がある.
b=a^3-a\ と\ b=-\,a\ を連立すると a^3-a=-\,a\ より\ \ a^3=0 よって\ \ a=0
3重解\ a=0\ をもつということは,\ a=0で接し,\ それ以外に共有点はもたない}ということである.
b=a^3-a\ のグラフを描くとき,\ 容易に因数分解できることに着目する.
この場合,\ 極値を求めるのではなく,\ a軸との交点を求めて図示する.
b=a^3-a=a(a^2-1)=a(a+1)(a-1)=0より,\ a=-\,1,\ 0,\ 1でa軸と交わる}とわかる.
a≠0かつ(a+b)(-\,a^3+a+b)<0としたが,\ 実際には(a+b)(-\,a^3+a+b)<0のみでよい.
a=0のときf(0)f(a)=\{f(0)\}^2≧0より,\ f(0)f(a)<0に矛盾する.
つまり,\ f(0)f(a)=(a+b)(-\,a^3+a+b)<0さえあれば,\ 自動的にa≠0といえるわけである.
前項で示した以下の引ける接線の本数の構図}を知っている人にとっては,\ 本問の結果は当然である.

