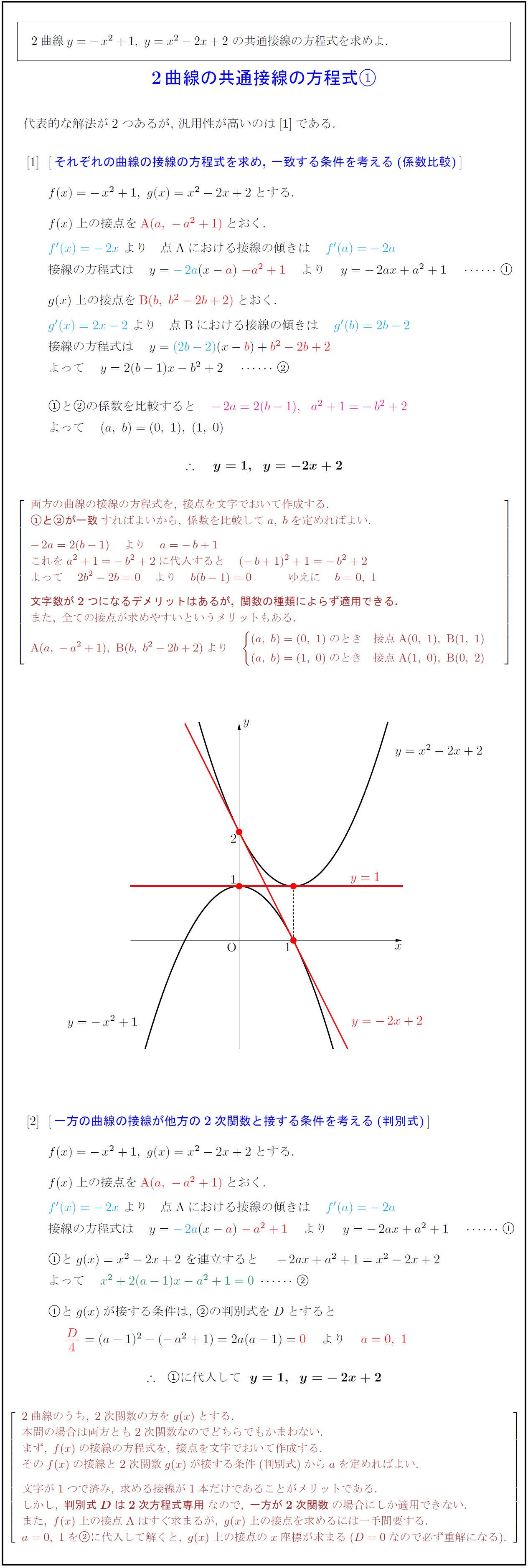
代表的な解法が2つあるが,\ 汎用性が高いのは[1]である. \,それぞれの曲線の接線の方程式を求め,\ 一致する条件を考える(係数比較)\,}
両方の曲線の接線の方程式を,\ 接点を文字でおいて作成する.
①と②が一致}すればよいから,\ 係数を比較してa,\ bを定めればよい.
文字数が2つになるデメリットはあるが,\ 関数の種類によらず適用できる.}
また,\ 全ての接点が求めやすいというメリットもある.
,一方の曲線の接線が他方の2次関数と接する条件を考える(判別式)\,]
2曲線のうち,\ 2次関数の方をg(x)とする.
本問の場合は両方とも2次関数なのでどちらでもかまわない.
まず,\ f(x)の接線の方程式を,\ 接点を文字でおいて作成する.
そのf(x)の接線と2次関数g(x)が接する条件(判別式)からaを定めればよい.
文字が1つで済み,\ 求める接線が1本だけであることがメリットである.
しかし,\ 判別式Dは2次方程式専用}なので,\ 一方が2次関数}の場合にしか適用できない.
また,\ f(x)上の接点 Aはすぐ求まるが,\ g(x)上の接点を求めるには一手間要する.
a=0,\ 1を②に代入して解くと,\ g(x)上の接点のx座標が求まる(D=0なので必ず重解になる).

