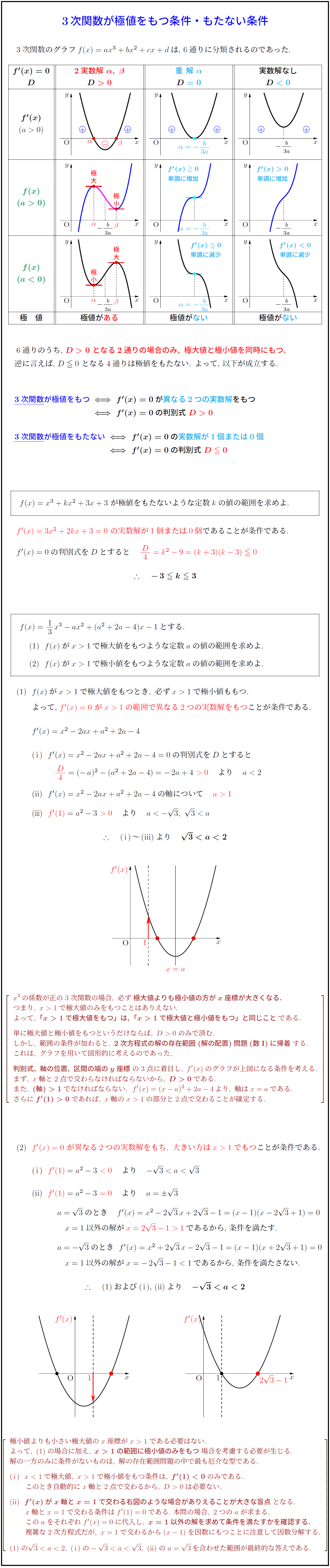
3次関数のグラフ$f(x)=ax^3+bx^2+cx+d$は,\ 6通りに分類されるのであった.
{2実数解{実数解なし\ となる2通りの場合のみ,\ 極大値と極小値を同時にもつ.$
逆に言えば,\ $D≦0$\ となる4通りは極値をもたない. よって,\ 以下が成立する.
3次関数}が極値をもつ$ f'(x)=0が異なる2つの実数解}をもつ}$
$f'(x)=0の判別式{3次関数}が極値をもたない$\{実数解が1個または0個$ 3\ が極値をもたないような定数kの値の範囲を求めよ.$の実数解が1個または0個}であることが条件である.$
$f'(x)=0$の判別式を$D$とすると $f(x)がx>1で極大値をもつような定数aの値の範囲を求めよ.$
(2)\ \ $f(x)がx>1で極小値をもつような定数aの値の範囲を求めよ.$ \\
必ずx>1で極小値ももつ.$\ がx>1の範囲で異なる2つの実数解をもつ}ことが条件である.$
x^3\,の係数が正の3次関数の場合,\ 必ず極大値よりも極小値の方がx座標が大きくなる.}
つまり,\ x>1で極大値のみをもつことはありえない.
よって,\ 「x>1で極大値をもつ」は,\ 「x>1で極大値と極小値をもつ」と同じこと}である.
単に極大値と極小値をもつというだけならば,\ D>0のみで済む.
しかし,\ 範囲の条件が加わると,\ 2次方程式の解の存在範囲(解の配置)問題(数I})に帰着}する.
これは,\ グラフを用いて図形的に考えるのであった.
判別式,\ 軸の位置,\ 区間の端のy座標}の3点に着目し,\ f'(x)のグラフが上図になる条件を考える.
まず,\ x軸と2点で交わらなければならないから,\ D>0}である.
また,\ (軸)>1}でなければならない.\ \ f'(x)=(x-a)^2+2a-4\,より,\ 軸はx=aである.
さらにf'(1)>0}であれば,\ x軸のx>1の部分と2点で交わることが確定する.
極小値よりも小さい極大値のx座標がx>1である必要はない.
よって,\ (1)の場合に加え,\ x>1の範囲に極小値のみをもつ}場合を考慮する必要が生じる.
解の一方のみに条件がないものは,\ 解の存在範囲問題の中で最も厄介な型である.
(.15zw}i.15zw})}\ \ x<1で極大値,\ x>1で極小値をもつ条件は,\ f'(-\,1)<0}のみである.
(ii)}\ \ このとき自動的にx軸と2点で交わるから,\ D>0は必要ない.
(ii)}\ \ f'(x)がx軸とx=1で交わる右図のような場合がありえることが大きな盲点}となる.
(ii)}\ \ x軸とx=1で交わる条件はf'(-\,1)=0である.\ 本問の場合,\ 2つのaが求まる.
(ii)}\ \ このaをそれぞれf'(x)=0に代入し,\ x=1以外の解を求めて条件を満たすかを確認する.}
(ii)}\ \ 複雑な2次方程式だが,\ x=1で交わるから(x-1)を因数にもつことに注意して因数分解する. を合わせた範囲が最終的な答えである.

