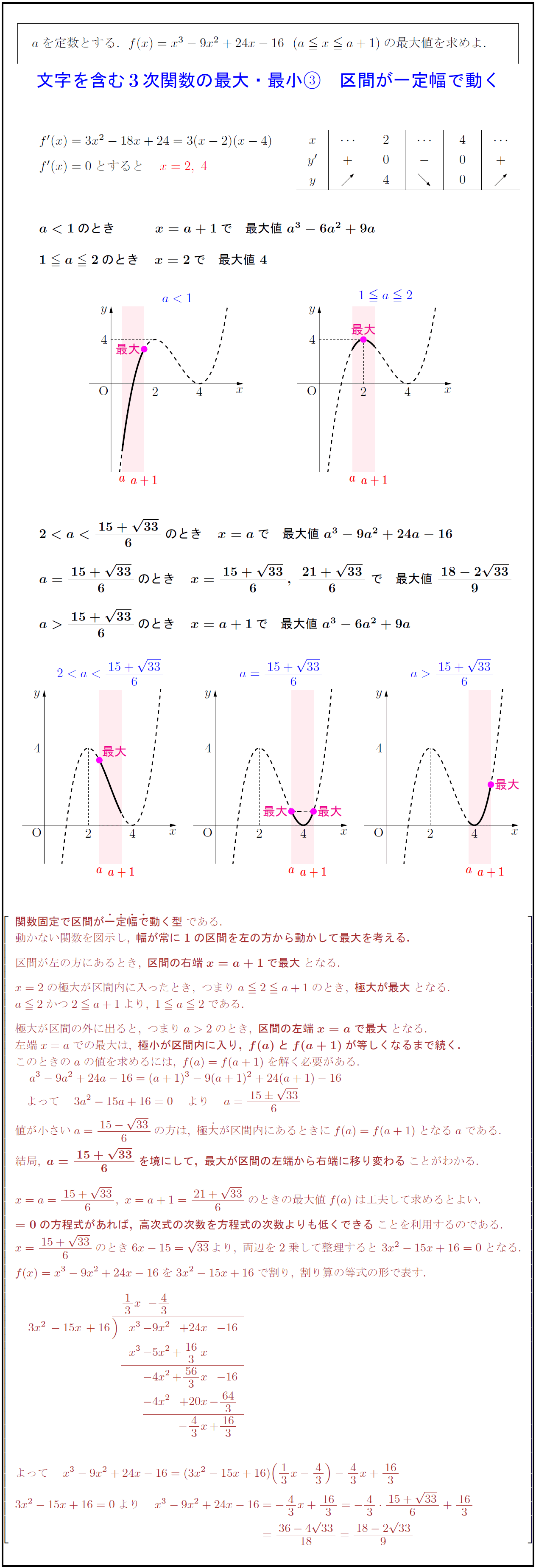
{関数固定で区間が\dot{一}\dot{定}\dot{幅}\dot{で}動く型}である.
動かない関数を図示し,\ 幅が常に1の区間を左の方から動かして最大を考える.}
区間が左の方にあるとき,\ 区間の右端x=a+1で最大}となる.
x=2の極大が区間内に入ったとき,\ つまりa≦2≦ a+1のとき,\ 極大が最大}となる.
a≦2かつ2≦ a+1より,\ 1≦ a≦2である.
極大が区間の外に出ると,\ つまりa>2のとき,\ 区間の左端x=aで最大}となる.
左端x=aでの最大は,\ 極小が区間内に入り,\ f(a)とf(a+1)が等しくなるまで続く.}
このときのaの値を求めるには,\ f(a)=f(a+1)を解く必要がある.
a^3-9a^2+24a-16=(a+1)^3-9(a+1)^2+24(a+1)-16
よって 3a^2-15a+16=0 より a=15±√{33{6}
値が小さいa=15-√{33{6}\,の方は,\ 極\dot{大}が区間内にあるときにf(a)=f(a+1)となるaである.
結局,\ a=15+√{33{6}\,を境にして,\ 最大が区間の左端から右端に移り変わる}ことがわかる.
x=a=15+√{33{6},\ x=a+1=21+√{33{6}\,のときの最大値f(a)は工夫して求めるとよい.
=0の方程式があれば,\ 高次式の次数を方程式の次数よりも低くできる}ことを利用するのである.
x=15+√{33{6}\,のとき6x-15=√{33}\,より,\ 両辺を2乗して整理すると\ 3x^2-15x+16=0となる.
f(x)=x^3-9x^2+24x-16を3x^2-15x+16で割り,\ 割り算の等式の形で表す.

