本項では,\ 実際に3次関数のグラフを図示する方法を学習する.
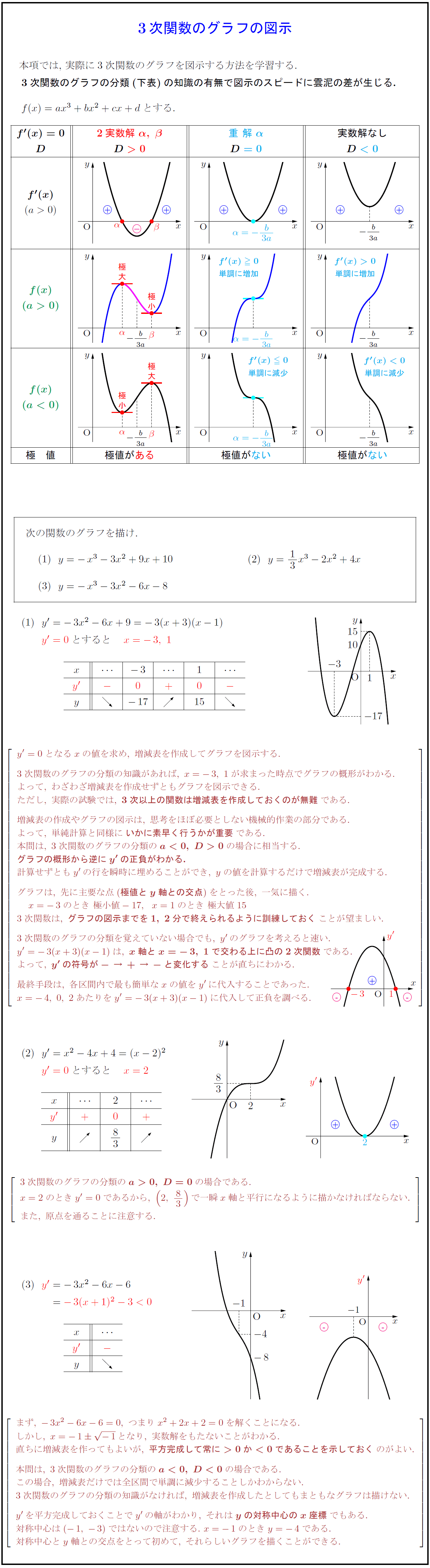
3次関数のグラフの分類(下表)の知識の有無で図示のスピードに雲泥の差が生じる.}
$f(x)=ax^3+bx^2+cx+d$とする.
y’=0となるxの値を求め,\ 増減表を作成してグラフを図示する.
3次関数のグラフの分類の知識があれば,\ x=-\,3,\ 1が求まった時点でグラフの概形がわかる.
よって,\ わざわざ増減表を作成せずともグラフを図示できる.
ただし,\ 実際の試験では,\ 3次以上の関数は増減表を作成しておくのが無難}である.
増減表の作成やグラフの図示は,\ 思考をほぼ必要としない機械的作業の部分である.
よって,\ 単純計算と同様にいかに素早く行うかが重要}である.
本問は,\ 3次関数のグラフの分類のa<0,\ D>0}の場合に相当する.
グラフの概形から逆にy’\,の正負がわかる.}
計算せずともy’\,の行を瞬時に埋めることができ,\ yの値を計算するだけで増減表が完成する.
グラフは,\ 先に主要な点(極値とy軸との交点})をとった後,\ 一気に描く.
x=-\,3のとき\ 極小値-17,\ \ x=1のとき\ 極大値15
3次関数は,\ グラフの図示までを1,\ 2分で終えられるように訓練しておく}ことが望ましい.
3次関数のグラフの分類を覚えていない場合でも,\ y’\,のグラフを考えると速い.
y’=-\,3(x+3)(x-1)は,\ x軸とx=-\,3,\ 1で交わる上に凸の2次関数}である.
よって,\ y’\,の符号が-\,→\,+\,→\,-と変化する}ことが直ちにわかる.
最終手段は,\ 各区間内で最も簡単なxの値をy’\,に代入することであった.
x=-\,4,\ 0,\ 2あたりをy’=-\,3(x+3)(x-1)に代入して正負を調べる. \\[-8zh]
3次関数のグラフの分類のa>0,\ D=0}の場合である.
x=2のときy’=0であるから,\ 2,\ 83で一瞬x軸と平行になるように描かなければならない.
また,\ 原点を通ることに注意する.
まず,\ -\,3x^2-6x-6=0,\ つまりx^2+2x+2=0を解くことになる.
しかし,\ x=-\,1±√{-\,1}\,となり,\ 実数解をもたないことがわかる.
直ちに増減表を作ってもよいが,\ 平方完成して常に>0か<0であることを示しておく}のがよい.
本問は,\ 3次関数のグラフの分類のa<0,\ D<0}の場合である.
この場合,\ 増減表だけでは全区間で単調に減少することしかわからない.
3次関数のグラフの分類の知識がなければ,\ 増減表を作成したとしてもまともなグラフは描けない.
y'\,を平方完成しておくことでy'\,の軸がわかり,\ それはyの対称中心のx座標}でもある.
対称中心は(-\,1,\ -\,3)ではないので注意する.\ x=-\,1のときy=-\,4である.
対称中心とy軸との交点をとって初めて,\ それらしいグラフを描くことができる.

