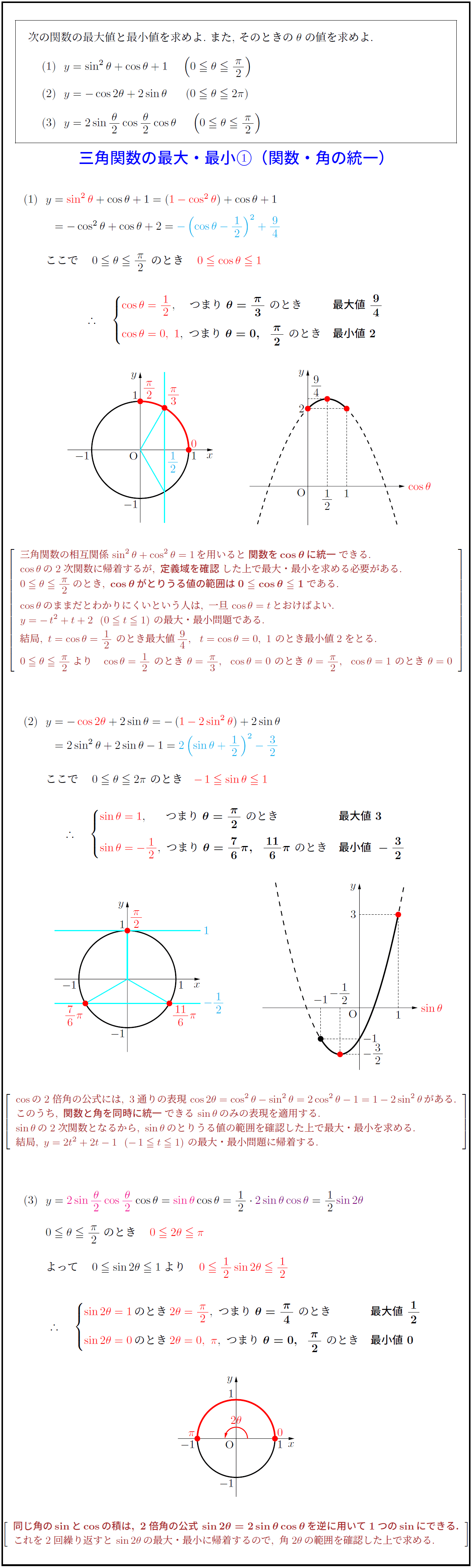
次の関数の最大値と最小値を求めよ.\ また,\ そのときの$θ$の値を求めよ. 三角関数の最大・最小①(関数・角の統一
三角関数の相互関係\,\sin^2θ+\cos^2θ=1\,を用いると関数を\cosθ\,に統一}できる.
\cosθ\,の2次関数に帰着するが,\ 定義域を確認}した上で最大・最小を求める必要がある.
0≦θ≦π}{2}\,のとき,\ \cosθ\,がとりうる値の範囲は0≦\cosθ≦1}である.
\cosθ\,のままだとわかりにくいという人は,\ 一旦\,\cosθ=t\,とおけばよい.
y=-\,t^2+t+2\ \ (0≦ t≦1)\ の最大・最小問題である.
結局,\ t=\cosθ=12\ のとき最大値\,94,\ \ t=\cosθ=0,\ 1\ のとき最小値2をとる.
\cos の2倍角の公式には,\ 3通りの表現\,\cos2θ=\cos^2θ-\sin^2θ=2\cos^2θ-1=1-2\sin^2θ\,がある.
このうち,\ 関数と角を同時に統一}できる\,\sinθ\,のみの表現を適用する.
\sinθ\,の2次関数となるから,\ \sinθ\,のとりうる値の範囲を確認した上で最大・最小を求める.
結局,\ y=2t^2+2t-1\ \ (-\,1≦ t≦1)\ の最大・最小問題に帰着する.
同じ角の \sin と \cos の積は,\ 2倍角の公式\,\sin2θ=2\sinθ\cosθ\,を逆に用いて1つの \sin にできる.}
これを2回繰り返すと\,\sin2θ\,の最大・最小に帰着するので,\ 角2θ\,の範囲を確認した上で求める.

