原点を出発点とし,\ $x$軸上を動く点Aがある.\ サイコロを1回振って3以上の目が \\[.2zh] \hspace{.5zw}出ると正の向きに1進み,\ 2以下の目が出ると負の向きに1進む. \\[.2zh] \hspace{.5zw}サイコロを6回振るとき,\ 次の確率を求めよ.\ (4)は条件付き確率の既習が前提である. \\[1zh] \hspace{.5zw} (1)\ \ 点Aが6回目に$x=5$にいる確率 \\[.8zh] \hspace{.5zw} (2)\ \ 点Aが6回目に$x\leqq2$にいる確率 \\[.8zh] \hspace{.5zw} (3)\ \ 点Aが2回目に原点に戻り,\ かつ6回目に原点に戻る確率 \\[.8zh] \hspace{.5zw} (4)\ \ 点Aが6回目に原点に戻ったとき,\ 2回目にも原点に戻っていた確率 \\[.8zh] \hspace{.5zw} (5)\ \ 点Aが途中で少なくとも1回原点に戻り,\ かつ6回目にも原点に戻る確率 \\ 反復試行による直線上の点の移動(ランダムウォーク)}}}} \\\\[.5zh] (1)\ \ 6回振るとき,\ \textcolor{forestgreen}{3以上の目が$x$回出る}とする. \\[.2zh] \phantom{ (1)}\ \ このとき,\ 点Aの座標は となる自然数xは存在しない}から,\ 求める確率は\ \ \bm{0}$ \\\\[1zh] (2)\ \ \textcolor{red}{$2x-6=2(x-3)$は偶数}であるから,\ 6回目に$x=(奇数)$にいることはない. \\[.2zh] \phantom{ (1)}\ \ よって,\ \textcolor{red}{$x\leqq2$の余事象は$x=4,\ 6$}であり,\ \ $\textcolor{red}{2x-6=4,\ 6}$のとき,\ $\textcolor{cyan}{x=5,\ 6}$である. (3)\ \ 3以上の目と2以下の目が同じ回数出るとき,\ 原点に戻る. \ (4)\ \ 6回目に原点に戻る事象を$A$,\ \ 2回目に原点に戻る事象を$B$とする. (5)\ \ 1\,～\,5回目に1回も原点に戻らない事象を$C$とする. 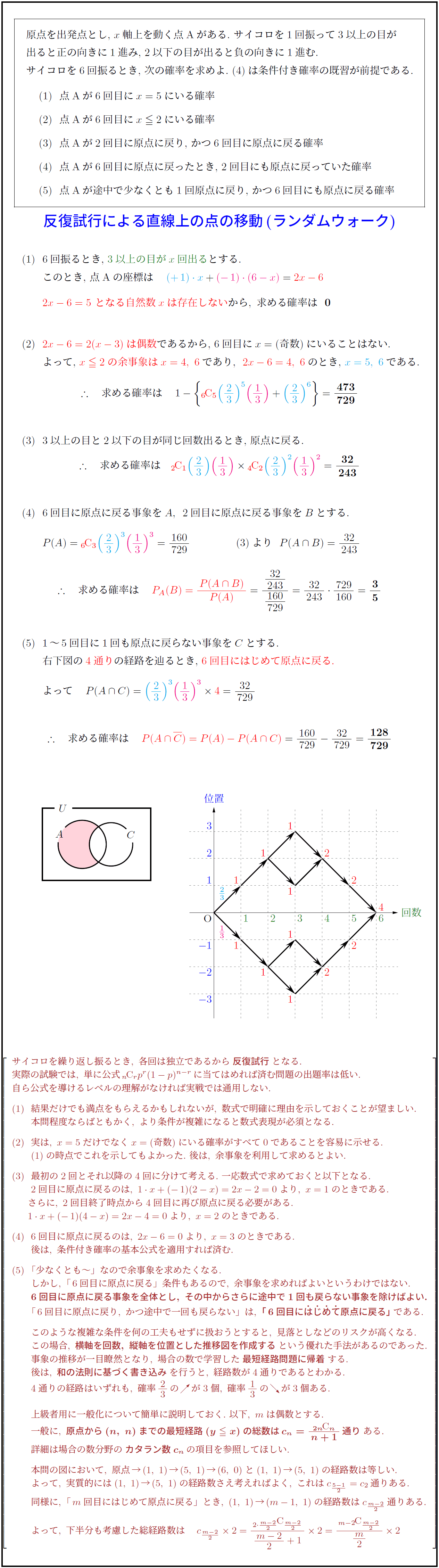\\[.2zh] \phantom{ (1)}\ \ 右下図の\textcolor{red}{4通り}の経路を辿るとき,\ \textcolor{red}{6回目にはじめて原点に戻る.} サイコロを繰り返し振るとき,\ 各回は独立であるから\bm{反復試行}となる. \\[.2zh] 実際の試験では,\ 単に公式\,\kumiawase nrp^r(1-p)^{n-r}\,に当てはめれば済む問題の出題率は低い. \\[.2zh] 自ら公式を導けるレベルの理解がなければ実戦では通用しない. \\[1zh] (1)\ \ 結果だけでも満点をもらえるかもしれないが,\ 数式で明確に理由を示しておくことが望ましい. \\[.2zh] \phantom{(1)}\ \ 本問程度ならばともかく,\ より条件が複雑になると数式表現が必須となる. \\[1zh] (2)\ \ 実は,\ x=5だけでなくx=(奇数)にいる確率がすべて0であることを容易に示せる. \\[.2zh] \phantom{(1)}\ \ (1)の時点でこれを示してもよかった.\ 後は,\ 余事象を利用して求めるとよい. \\[1zh] (3)\ \ 最初の2回とそれ以降の4回に分けて考える.\ 一応数式で求めておくと以下となる. \\[.2zh] \phantom{(1)}\ \ 2回目に原点に戻るのは,\ 1\cdot x+(-\,1)(2-x)=2x-2=0より,\ x=1のときである. \\[.2zh] \phantom{(1)}\ さらに,\ 2回目終了時点から4回目に再び原点に戻る必要がある. \\[.2zh] \phantom{(1)}\ 1\cdot x+(-\,1)(4-x)=2x-4=0より,\ x=2のときである. \\[1zh] (4)\ \ 6回目に原点に戻るのは,\ 2x-6=0より,\ x=3のときである. \\[.2zh] \phantom{(1)}\ \ 後は,\ 条件付き確率の基本公式を適用すれば済む. \\[1zh] (5)\ \ 「少なくとも～」なので余事象を求めたくなる. \\[.2zh] \phantom{(1)}\ \ しかし,\ 「\,6回目に原点に戻る」条件もあるので,\ 単に余事象を求めれば済むわけではない. \\[.2zh] \phantom{(1)}\ \ \bm{6回目に原点に戻る事象を全体とし,\ その中からさらに途中で1回も戻らない事象を除けばよい.} \\[.2zh] \phantom{(1)}\ \ 「\,6回目に原点に戻り,\ かつ途中で一回も戻らない」は,\ \bm{「\,6回目に\dot{は}\dot{じ}\dot{め}\dot{て}原点に戻る」}である. \\[1zh] \phantom{(1)}\ \ このような複雑な条件を何の工夫もせずに扱おうとすると,\ 見落としなどのリスクが高くなる. \\[.2zh] \phantom{(1)}\ \ この場合,\ \bm{横軸を回数,\ 縦軸を位置とした推移図を作成する}という優れた手法があるのであった. \\[.2zh] \phantom{(1)}\ \ 事象の推移が一目瞭然となり,\ 場合の数で学習した\bm{最短経路問題に帰着}する. \\[.2zh] \phantom{(1)}\ \ 後は,\ \bm{和の法則に基づく書き込み}を行うと,\ 経路数が4通りであるとわかる. \\[.2zh] \phantom{(1)}\ \ 4通りの経路はいずれも,\ 確率\,\bunsuu23\,の\,\NE\,が3個,\ 確率\,\bunsuu13\,の\,\SE\,が3個ある. \\\\ \phantom{(1)}\ \ 上級者用に一般化について簡単に説明しておく.\ 以下,\ mは偶数とする. \\[.2zh] \phantom{(1)}\ \ 一般に,\ \bm{原点から(n,\ n)までの最短経路(y\leqq x)の総数は\,c_n=\bunsuu{\kumiawase{2n}{n}}{n+1}\,通り}ある. \\[.8zh] \phantom{(1)}\ \ 詳細は場合の数分野の\bm{カタラン数c_n}\,の項目を参照してほしい. \\[1zh] \phantom{(1)}\ \ 本問の図において,\ 原点\,→\,(1,\ 1)\,→\,(5,\ 1)\,→\,(6,\ 0)と(1,\ 1)\,→\,(5,\ 1)の経路数は等しい. \\[.2zh] \phantom{(1)}\ \ よって,\ 実質的には(1,\ 1)\,→\,(5,\ 1)の経路数さえ考えればよく,\ これはc_{\frac{5-1}{2}}=c_2\,通りある. \\[.8zh] \phantom{(1)}\ \ 同様に,\ 「\,m回目にはじめて原点に戻る」とき,\ (1,\ 1)\,→\,(m-1,\ 1)の経路数はc_{\frac{m-2}{2}}\,通りある. \\[1zh] \phantom{(1)}\ \ よって,\ 下半分も考慮した総経路数は
