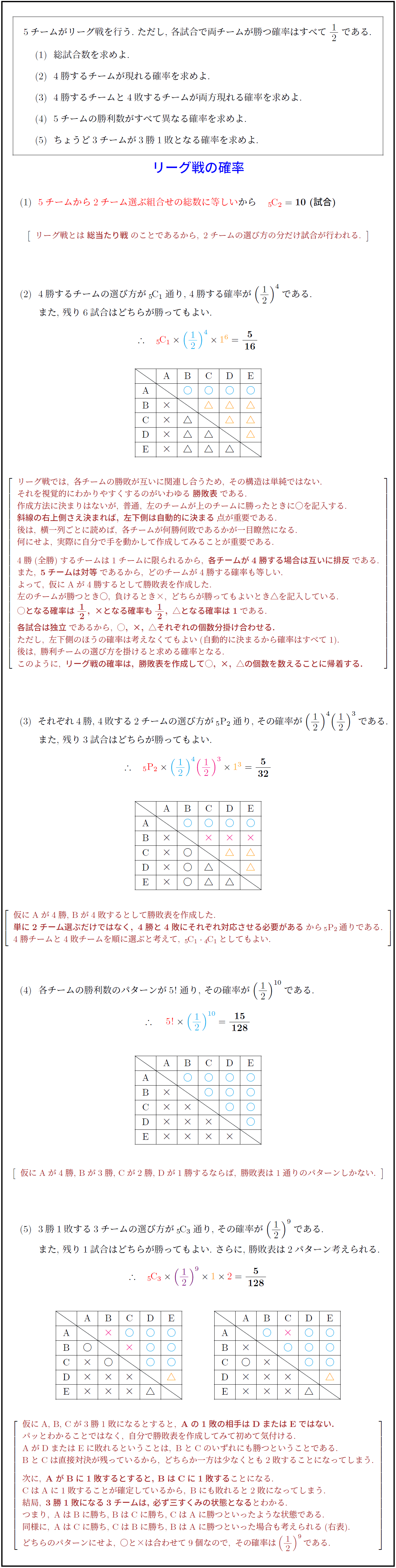
5チームがリーグ戦を行う.\ ただし,\ 各試合で両チームが勝つ確率はすべて$12$である.
(1)\ \ 総試合数を求めよ.
(2)\ \ 4勝するチームが現れる確率を求めよ.
(3)\ \ 4勝するチームと4敗するチームが両方現れる確率を求めよ.
(4)\ \ 5チームの勝利数がすべて異なる確率を求めよ.
(5)\ \ ちょうど3チームが3勝1敗となる確率を求めよ. \\
リーグ戦の確率 \\
(1)\ \ 5チームから2チーム選ぶ組合せの総数に等しい}から $C52}=10\ (試合)}$
リーグ戦とは総当たり戦}のことであるから,\ 2チームの選び方の分だけ試合が行われる.
4勝するチームの選び方が$C51$通り,\ 4勝する確率が$12^4$である.
また,\ 残り6試合はどちらが勝ってもよい.
リーグ戦では,\ 各チームの勝敗が互いに関連し合うため,\ その構造は単純ではない.
それを視覚的にわかりやすくするのがいわゆる勝敗表}である.
作成方法に決まりはないが,\ 普通,\ 左のチームが上のチームに勝ったときに○を記入する.
斜線の右上側さえ決まれば,\ 左下側は自動的に決まる}点が重要である.
後は,\ 横一列ごとに読めば,\ 各チームが何勝何敗であるかが一目瞭然になる.
何にせよ,\ 実際に自分で手を動かして作成してみることが重要である.
4勝(全勝)するチームは1チームに限られるから,\ 各チームが4勝する場合は互いに排反}である.
また,\ 5チームは対等}であるから,\ どのチームが4勝する確率も等しい.
よって,\ 仮に Aが4勝するとして勝敗表を作成した.
左のチームが勝つとき○,\ 負けるとき×,\ どちらが勝ってもよいとき△を記入している.
○となる確率は\,12,\ ×となる確率も\,12,\ △となる確率は1}である.
各試合は独立}であるから,\ ○,\ ×,\ △それぞれの個数分掛け合わせる.}
ただし,\ 左下側のほうの確率は考えなくてもよい(自動的に決まるから確率はすべて1).
後は,\ 勝利チームの選び方を掛けると求める確率となる.
このように,\ リーグ戦の確率は,\ 勝敗表を作成して○,\ ×,\ △の個数を数えることに帰着する.}
それぞれ4勝,\ 4敗する2チームの選び方が$P52$通り,\ その確率がまた,\ 残り3試合はどちらが勝ってもよい.
仮にAが4勝,\ Bが4敗}するとして勝敗表を作成した.
単に2チーム選ぶだけではなく,\ 4勝と4敗にそれぞれ対応させる必要がある}から\,P52\,通りである.
4勝チームと4敗チームを順に選ぶと考えて,\ C51・C41\,としてもよい.
\end{array\right]$ \\
(4)\ \ 各チームの勝利数のパターンが$5!$通り,\ その確率が$12^{10}$である. \\[
仮にAが4勝,\ Bが3勝,\ Cが2勝,\ Dが1勝}するならば,\ 勝敗表は1通りのパターンしかない.
3勝1敗する3チームの選び方が$C53$通り,\ その確率が$12^9$である.
また, 残り1試合はどちらが勝ってもよい.\ さらに,\ 勝敗表は2パターン考えられる.
仮にA,\ B,\ C}が3勝1敗になるとすると,\ Aの1敗の相手はDまたはE}ではない.}
パッとわかることではなく,\ 自分で勝敗表を作成してみて初めて気付ける.
AがDまたはE}に敗れるということは,\ BとC}のいずれにも勝つということである.
BとC}は直接対決が残っているから,\ どちらか一方は少なくとも2敗することになってしまう.
次に,\ AがBに1敗するとすると,\ BはCに1敗する}ことになる.
Cは Aに1敗することが確定しているから,\ Bにも敗れると2敗になってしまう.
結局,\ 3勝1敗になる3チームは,\ 必ず三すくみの状態となる}とわかる.
つまり,\ AはBに勝ち,\ BはCに勝ち,\ CはAに勝つ}といったような状態である.
同様に,\ AはCに勝ち,\ CはBに勝ち,\ BはAに勝つ}といった場合も考えられる(右表).
どちらのパターンにせよ,\ ○と×は合わせて9個なので,\ その確率は12^9である.

