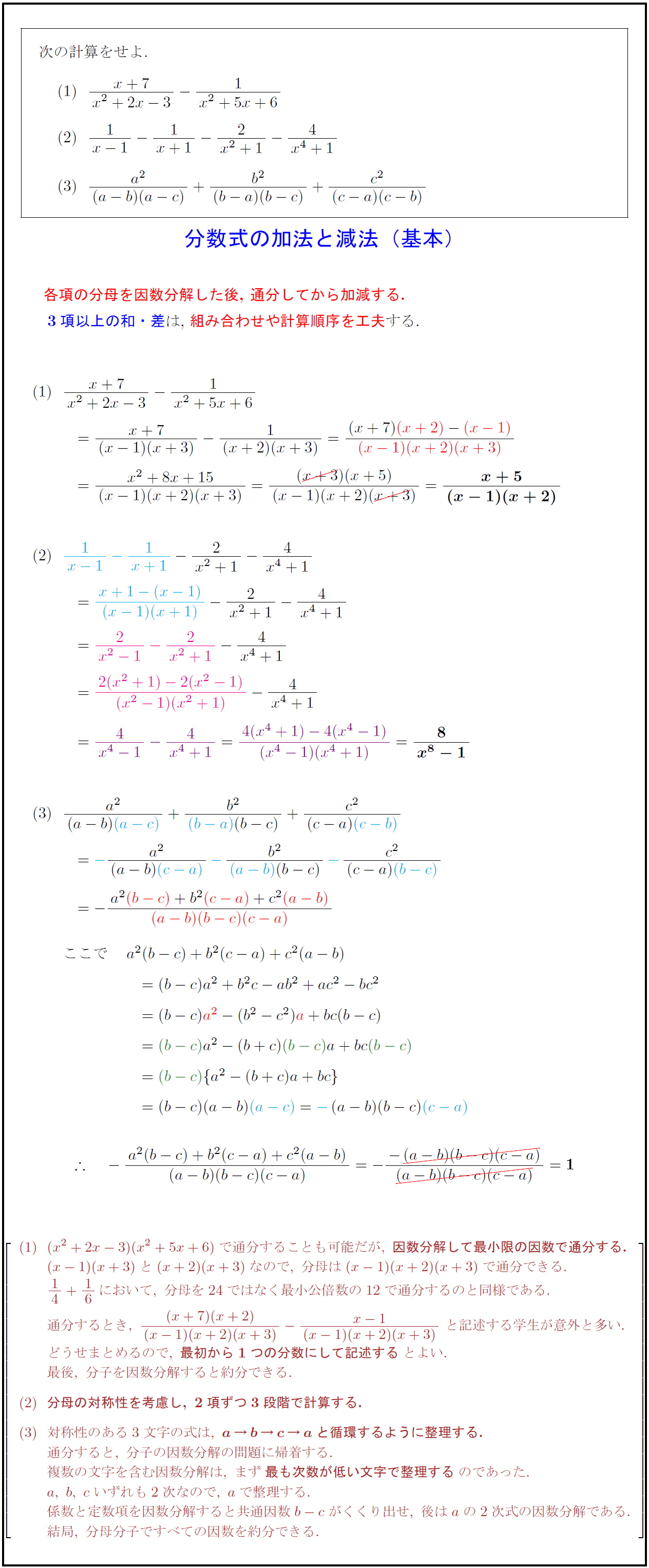
各項の分母を因数分解した後,\ 通分してから加減する.
3項以上の和・差は,\ 組み合わせや計算順序を工夫する.
(1)\ \ (x^2+2x-3)(x^2+5x+6)で通分することも可能だが,\ 因数分解して最小限の因数で通分する.}
\ \ (x-1)(x+3)と(x+2)(x+3)なので,\ 分母は(x-1)(x+2)(x+3)で通分できる.
\ \ 14+16\,において,\ 分母を24ではなく最小公倍数の12で通分するのと同様である.
\ \ 通分するとき,\ \ と記述する学生が意外と多い.
\ \ どうせまとめるので,\ 最初から1つの分数にして記述する}とよい.
\ \ 最後,\ 分子を因数分解すると約分できる.
(2)\ \ 分母の対称性を考慮し,\ 2項ずつ3段階で計算する.}
(3)\ \ 対称性のある3文字の式は,\ a\,→\,b\,→\,c\,→\,aと循環するように整理する.}
\ \ 通分すると,\ 分子の因数分解の問題に帰着する.
\ \ 複数の文字を含む因数分解は,\ まず最も次数が低い文字で整理する}のであった.
\ \ a,\ b,\ cいずれも2次なので,\ aで整理する.
\ \ 係数と定数項を因数分解すると共通因数b-cがくくり出せ,\ 後はaの2次式の因数分解である.
\ \ 結局,\ 分母分子ですべての因数を約分できる.

