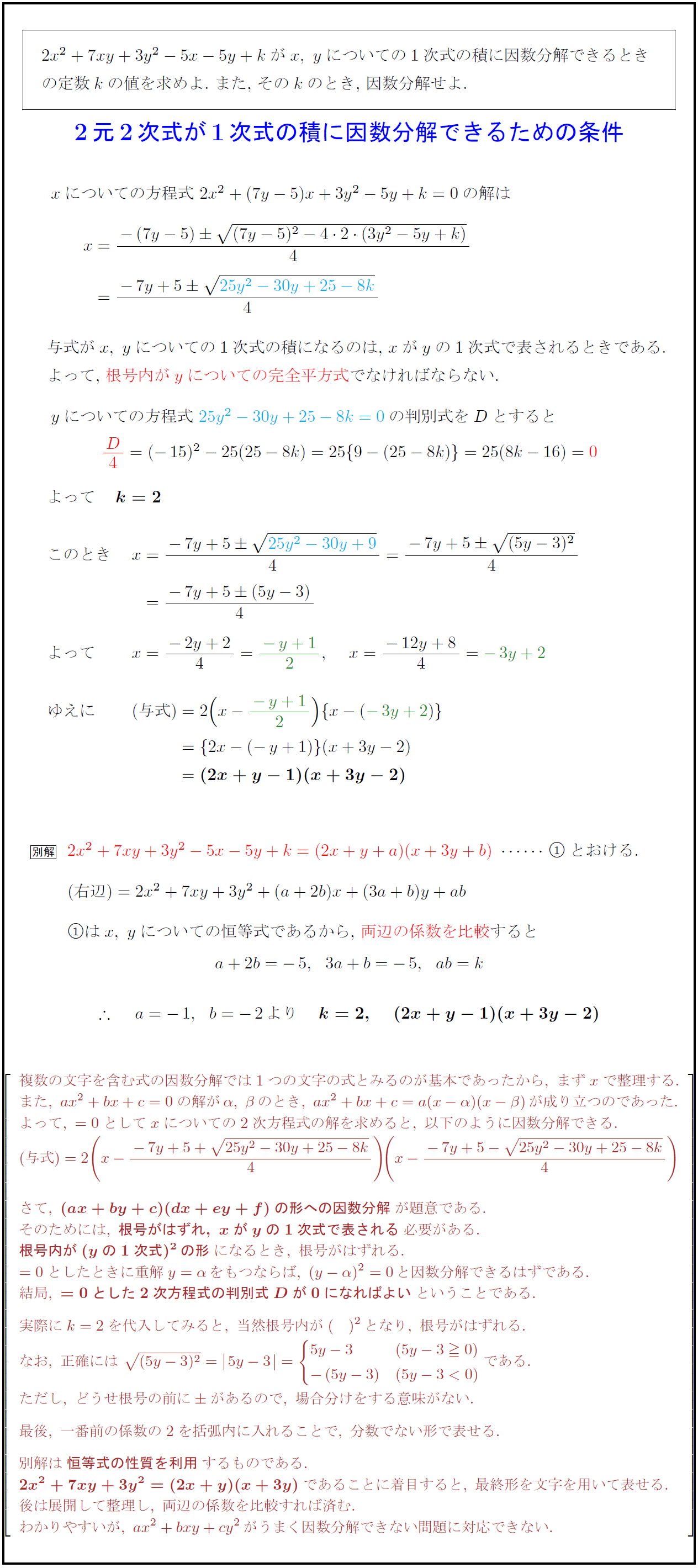
2x^2+7xy+3y^2-5x-5y+k$が$x,\ y$についての1次式の積に因数分解できるとき
の定数$k$の値を求めよ.\ また,\ その$k$のとき,\ 因数分解せよ. \\
{2元2次式が1次式の積に因数分解できるための条件}$ \\
$x$についての方程式\ $2x^2+(7y-5)x+3y^2-5y+k=0$の解は
与式が$x,\ y$についての1次式の積になるのは,\ $x$が$y$の1次式で表されるときである.
よって,\ 根号内が$y$についての完全平方式}でなければならない.
$y$についての方程式\ $25y^2-30y+25-8k=0}$の判別式を$D$とすると \\$x,\ y$についての恒等式であるから,\ 両辺の係数を比較
複数の文字を含む式の因数分解では1つの文字の式とみるのが基本であったから,\ まずxで整理する.
また,\ ax^2+bx+c=0の解が\,α,\ β\,のとき,\ ax^2+bx+c=a(x-α)(x-β)\,が成り立つのであった.
よって,\ =0としてxについての2次方程式の解を求めると,\ 以下のように因数分解できる.
さて,\ (ax+by+c)(dx+ey+f)の形への因数分解}が題意である.
そのためには,\ 根号がはずれ,\ xがyの1次式で表される}必要がある.
根号内が(yの1次式)^2\,の形}になるとき,\ 根号がはずれる.
=0としたときに重解y=α\,をもつならば,\ (y-α)^2=0\,と因数分解できるはずである.
結局,\ =0とした2次方程式の判別式Dが0になればよい}ということである.
実際にk=2を代入してみると,\ 当然根号内が( )^2\,となり,\ 根号がはずれる.
なお,\ 正確には
ただし,\ どうせ根号の前に ± があるので,\ 場合分けをする意味がない.
最後,\ 一番前の係数の2を括弧内に入れることで,\ 分数でない形で表せる.
別解は恒等式の性質を利用}するものである.
2x^2+7xy+3y^2=(2x+y)(x+3y)}であることに着目すると,\ 最終形を文字を用いて表せる.
後は展開して整理し,\ 両辺の係数を比較すれば済む.
わかりやすいが,\ ax^2+bxy+cy^2\,がうまく因数分解できない問題に対応できない.

