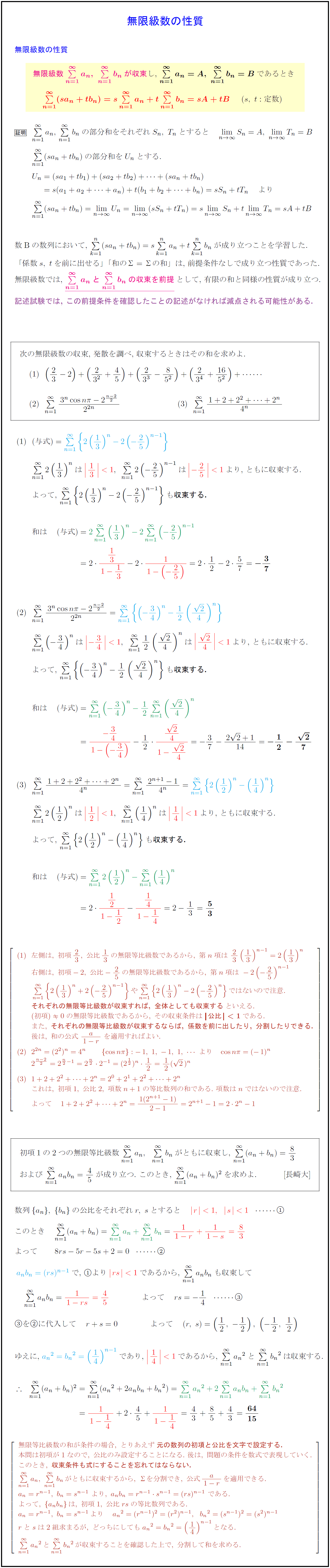
無限級数の性質}{無限級数${Σa_n,\ Σb_n}$が収束し,\ ${Σa_n=A,\ Σb_n=B}$であるとき ${Σ(sa_n+tb_n)=sΣa_n+tΣb_n=sA+tB (s,\ t:定数)$}b_n$の部分和をそれぞれ$S_n,\ T_n$とすると $lim[n→∞]S_n=A,\ lim[n→∞]T_n=B$ { }$Σ(sa_n+tb_n)$の部分和を$U_n$とする. [ 数Bの数列において,\ $Σ(sa_n+tb_n)=sΣa_n+tΣb_n$が成り立つことを学習した. 「係数$s,\ t$を前に出せる」「和のΣ$=$Σの和」は,\ 前提条件なしで成り立つ性質であった. 無限級数では,\ ${Σa_n}$と${Σb_n}$の収束を前提}として,\ 有限の和と同様の性質が成り立つ. 記述試験では,\ この前提条件を確認したことの記述がなければ減点される可能性がある. 次の無限級数の収束,\ 発散を調べ,\ 収束するときはその和を求めよ. 左側は,\ 初項23,\ 公比13の無限等比級数であるから,\ 第n項は\ 23(13)^{n-1}=2(13)^n 右側は,\ 初項-2,\ 公比-25の無限等比級数であるから,\ 第n項は\ -2ではないので注意. {それぞれの無限等比級数が収束すれば,\ 全体としても収束する}といえる. (初項)0の無限等比級数であるから,\ その収束条件は{公比}<1}である. また,\ {それぞれの無限等比級数が収束するならば,\ 係数を前に出したり,\ 分割したりできる.} 後は,\ 和の公式\ {a}{1-r}\ を適用すればよい. \ これは,\ 初項1,\ 公比2,\ 項数n+1の等比数列の和である.\ 項数はnではないので注意. w}初項1の2つの無限等比級数$Σa_n,Σb_n$がともに収束し,\ $Σ(a_n+b_n)=83$ および\ $Σa_nb_n=45$が成り立つ.\ このとき,\ $Σ(a_n+b_n)²$を求めよ. [長崎大] \ 数列${a_n},\ {b_n}$の公比をそれぞれ$r,\ s$とすると 無限等比級数の和が条件の場合,\ とりあえず{元の数列の初項と公比を文字で設定する.} 本問は初項が1なので,\ 公比のみ設定することになる.\ 後は,\ 問題の条件を数式で表現していく. このとき,\ {収束条件も式にすることを忘れてはならない.} Σa_n,\ Σb_nがともに収束するから,\ Σを分割でき,\ 公式{a}{1-r}を適用できる. よって,\ {a_nb_n}は,\ 初項1,\ 公比rsの等比数列である. rとsは2組求まるが,\ どっちにしても{a_n}²={b_n}²=(14)^{n-1}となる. Σ{a_n}²とΣ{b_n}²が収束することを確認した上で,\ 分割して和を求める.

