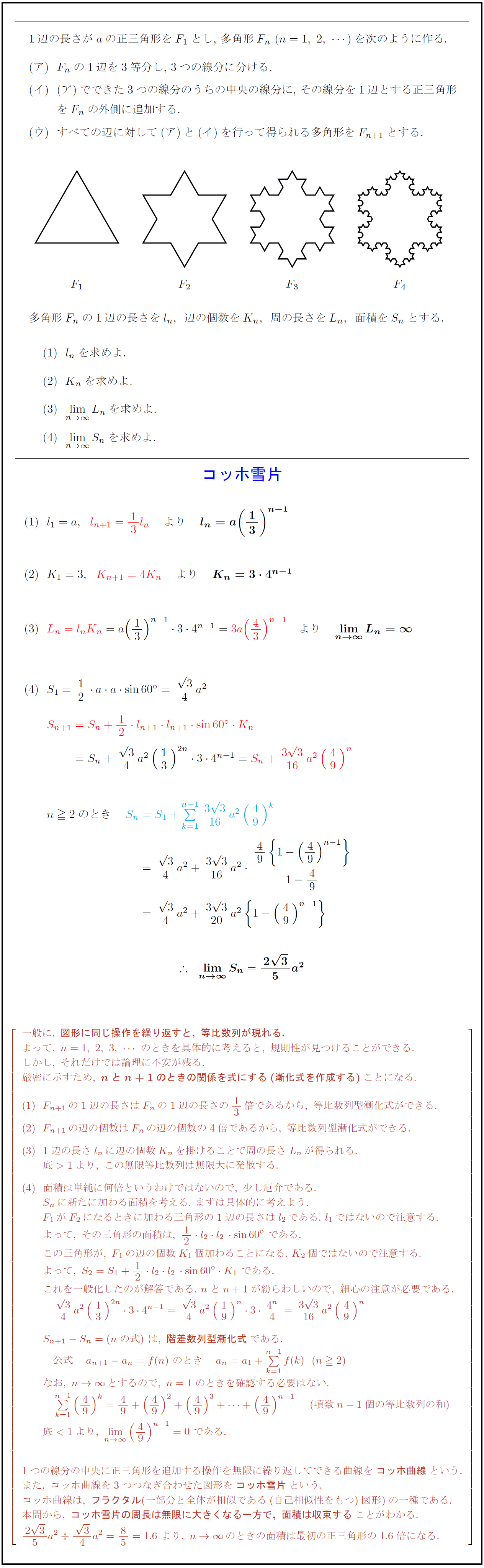
}1辺の長さが$a$の正三角形を$F₁$とし,\ 多角形$F_n\ (n=1,\ 2,\ )$を次のように作る. (ア)$F_n$の1辺を3等分し,\ 3つの線分に分ける. (イ)(ア)でできた3つの線分のうちの中央の線分に,\ その線分を1辺とする正三角形 {(イ)}を$F_n$の外側に追加する. (ウ)すべての辺に対して(ア)と(イ)を行って得られる多角形を$F_{n+1}$とする. 一般に,\ {図形に同じ操作を繰り返すと,\ 等比数列が現れる.} よって,\ n=1,\ 2,\ 3,のときを具体的に考えると,\ 規則性が見つけることができる. しかし,\ それだけでは論理に不安が残る. 厳密に示すため,\ {nとn+1のときの関係を式にする(漸化式を作成する)}ことになる. F_{n+1}の1辺の長さはF_nの1辺の長さの13倍であるから,\ 等比数列型漸化式ができる. F_{n+1}の辺の個数はF_nの辺の個数の4倍であるから,\ 等比数列型漸化式ができる. 1辺の長さl_nに辺の個数K_nを掛けることで周の長さL_nが得られる. 底>1より,\ この無限等比数列は無限大に発散する. 面積は単純に何倍というわけではないので,\ 少し厄介である. S_nに新たに加わる面積を考える.\ まずは具体的に考えよう. F₁がF₂になるときに加わる三角形の1辺の長さはl₂である.\ l₁ではないので注意する. よって,\ その三角形の面積は,\ 12 l₂ l₂sin60°\ である. この三角形が,\ F₁の辺の個数K₁個加わることになる.\ K₂個ではないので注意する. よって,\ S₂=S₁+12 l₂ l₂sin60° K₁\ である. これを一般化したのが解答である.\ nとn+1が紛らわしいので,\ 細心の注意が必要である. S_{n+1}-S_n=(nの式)\ は,\ {階差数列型漸化式}である. 公式 a_{n+1}-a_n=f(n)\ のとき a_n=a₁+n-1}f(k)(n2) なお,\ n→∞とするので,\ n=1のときを確認する必要はない. 1} (項数n-1個の等比数列の和)\ 底<1より,\ lim[n→∞](49)^{n-1}=0\ である. 1つの線分の中央に正三角形を追加する操作を無限に繰り返してできる曲線を{コッホ曲線}という. また,\ コッホ曲線を3つつなぎ合わせた図形を{コッホ雪片}という. コッホ曲線は,\ {フラクタル}(一部分と全体が相似である(自己相似性をもつ)図形)の一種である. 本問から,\ {コッホ雪片の周長は無限に大きくなる一方で,\ 面積は収束する}ことがわかる. {23}{5}a²{3}{4}a²=85=1.6\ より,\ n→∞のときの面積は最初の正三角形の1.6倍になる.

