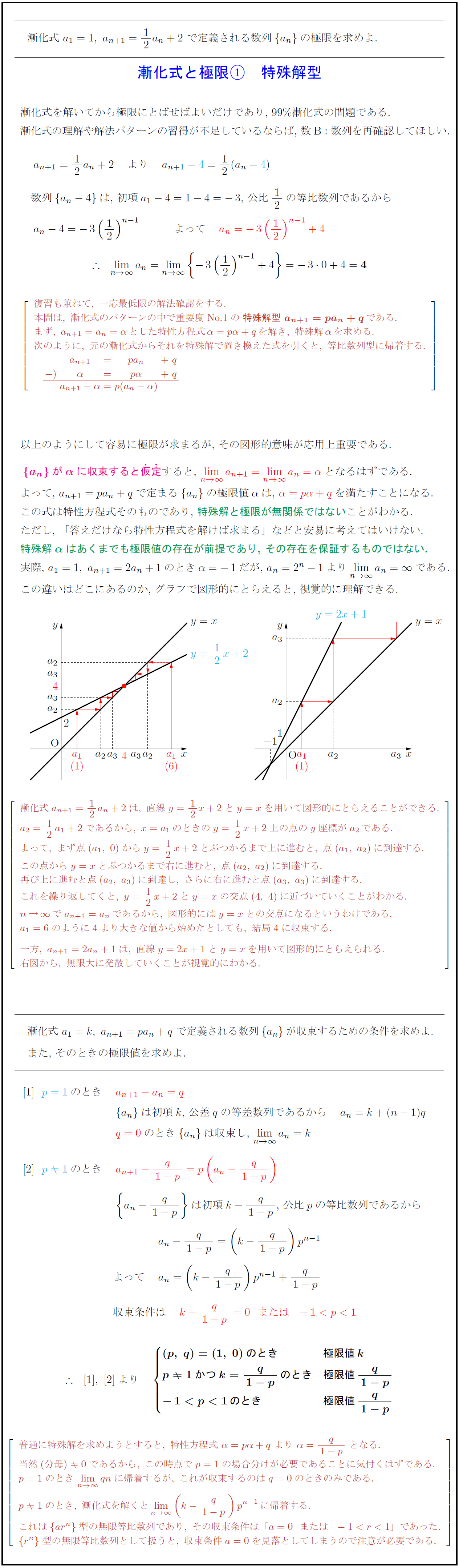
漸化式\ $a₁=1,\ a_{n+1}=12a_n+2$\ で定義される数列${a_n}$の極限を求めよ. 漸化式と極限 特殊解型 漸化式を解いてから極限にとばせばよいだけであり,\ 99\%漸化式の問題である. 漸化式の理解や解法パターンの習得が不足しているならば,\ 数B:数列を再確認してほしい. 数列${a_n-4}$は,\ 初項$a₁-4=1-4=-3$,\ 公比$12$の等比数列であるから 復習も兼ねて,\ 一応最低限の解法確認をする. 本問は,\ 漸化式のパターンの中で重要度No.1}の{特殊解型\ a_{n+1}=pa_n+q}である. まず,\ a_{n+1}=a_n=αとした特性方程式α=pα+qを解き,\ 特殊解αを求める. 次のように,\ 元の漸化式からそれを特殊解で置き換えた式を引くと,\ 等比数列型に帰着する. 以上のようにして容易に極限が求まるが,\ その図形的意味が応用上重要である. $a_n$が${α}$に収束すると{仮}{定}すると,\ $lim[n→∞]a_{n+1}=lim[n→∞]a_n=α}$となるはずである. よって,\ $a_{n+1}=pa_n+q$で定まる${a_n}$の極限値$α$は,\ $α=pα+q}$を満たすことになる. この式は特性方程式そのものであり,\ 特殊解と極限が無関係ではないことがわかる. ただし,\ 「答えだけなら特性方程式を解けば求まる」などと安易に考えてはいけない. 特殊解${α}$はあくまでも極限値の存在が前提であり,\ その存在を保証するものではない. 実際,\ $a₁=1,\ a_{n+1}=2a_n+1$のとき$α=-1$だが,\ $a_n=2^{n}-1$より$lim[n→∞]a_n=∞$である. この違いはどこにあるのか,\ グラフで図形的にとらえると,\ 視覚的に理解できる. \ 漸化式a_{n+1}=12a_n+2は,\ 直線y=12x+2とy=xを用いて図形的にとらえることができる. a₂=12a₁+2であるから,\ x=a₁のときのy=12x+2上の点のy座標がa₂である. よって,\ まず点(a₁,\ 0)からy=12x+2とぶつかるまで上に進むと,\ 点(a₁,\ a₂)に到達する. この点からy=xとぶつかるまで右に進むと,\ 点(a₂,\ a₂)に到達する. 再び上に進むと点(a₂,\ a₃)に到達し,\ さらに右に進むと点(a₃,\ a₃)に到達する. これを繰り返してくと,\ y=12x+2とy=xの交点(4,\ 4)に近づいていくことがわかる. n→∞でa_{n+1}=a_nであるから,\ 図形的にはy=xとの交点になるというわけである. a₁=6のように4より大きな値から始めたとしても,\ 結局4に収束する. 一方,\ a_{n+1}=2a_n+1は,\ 直線y=2x+1とy=xを用いて図形的にとらえられる. 右図から,\ 無限大に発散していくことが視覚的にわかる.

