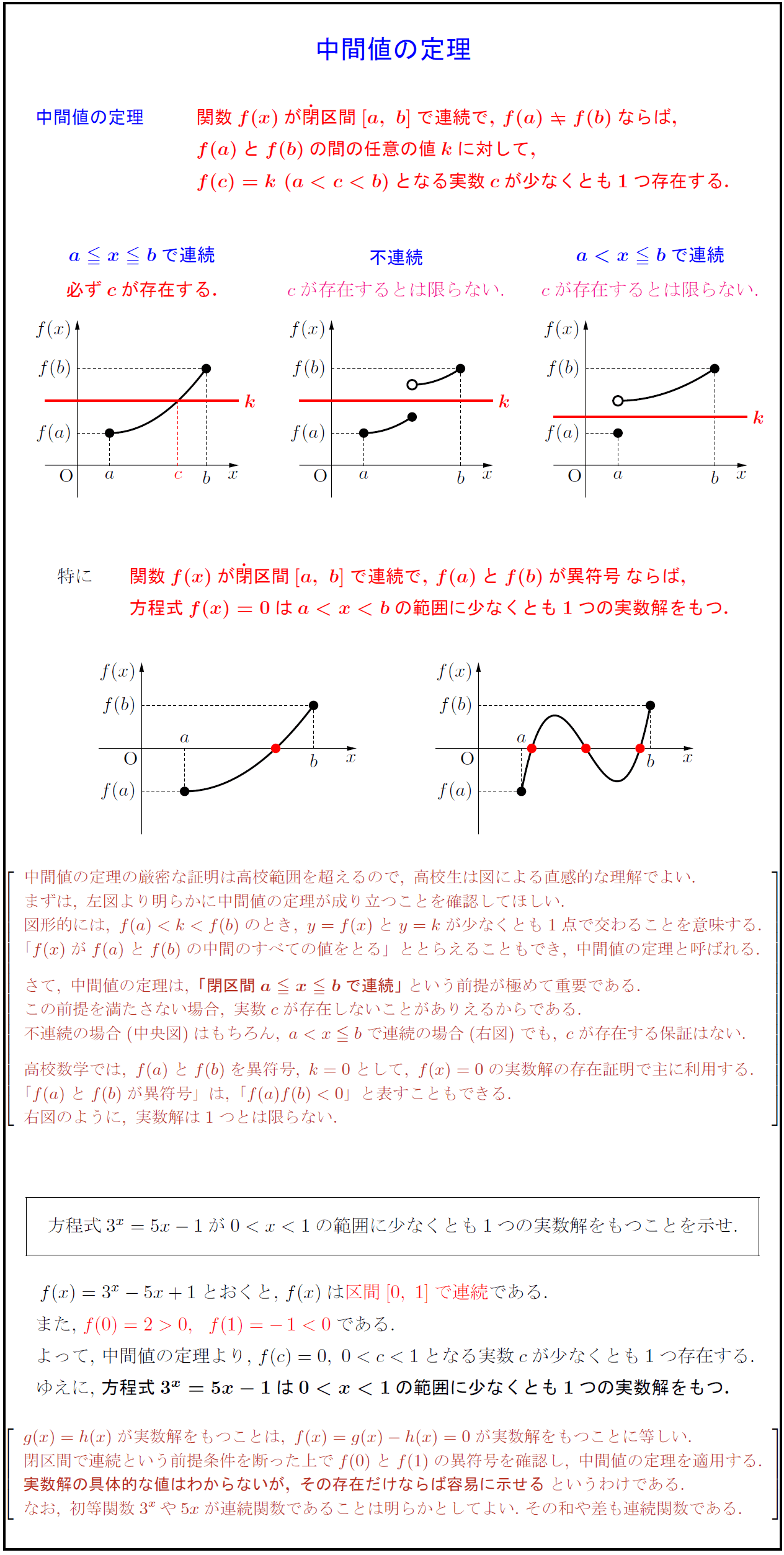
中間値の定理 関数${f(x)}$が{閉}区間${[a,\ b]}$で連続で,\ ${f(a) f(b)}$ならば, ${f(a)とf(b)}$の間の任意の値${k}$に対して,\ ${f(c)=k\ となる実数${c}$が少なくとも1つ存在する. {$c$が存在するとは限らない.}b}$で連続}=”” 特に 関数${f(x)}$が{閉}区間${[a,\=”” b]}$で連続で,\=”” ${f(a)とf(b)が異符号}$ならば,=”” 方程式${f(x)=”0}$はの範囲に少なくとも1つの実数解をもつ.” 中間値の定理の厳密な証明は高校範囲を超えるので,\=”” 高校生は図による直感的な理解でよい.=”” まずは,\=”” 左図より明らかに中間値の定理が成り立つことを確認してほしい.=”” 図形的には,\=”” のとき,\=”” y=”f(x)とy=kが少なくとも1点で交わることを意味する.” 「f(x)がf(a)とf(b)の中間のすべての値をとる」ととらえることもでき,\=”” 中間値の定理と呼ばれる.=”” さて,\=”” 中間値の定理は,\=”” {「閉区間a=”” x=”” bで連続」}という前提が極めて重要である.=”” この前提を満たさない場合,\=”” 実数cが存在しないことがありえるからである.=”” 不連続の場合(中央図)はもちろん,\=”” で連続の場合(右図)でも,\=”” cが存在する保証はない.=”” 高校数学では,\=”” f(a)とf(b)を異符号,\=”” k=”0として,\” f(x)=”0の実数解の存在証明で主に利用する.” 「f(a)とf(b)が異符号」は,\=”” 「f(a)f(b)<0」と表すこともできる.=”” 右図のように,\=”” 実数解は1つとは限らない.=”” 方程式$3^x=”5x-1$が$0<x<1$の範囲に少なくとも1つの実数解をもつことを示せ.” [-.8zh]=”” $f(x)=”3^x-5x+1$とおくと,\” $f(x)$は区間$[0,\=”” 1]$で連続}である.=”” また,\=”” $f(0)=”2″ 0,f=”-1<0$}である." よって,\="" 中間値の定理より,\="" $f(c)="0,\" となる実数$c$が少なくとも1つ存在する.="" ゆえに,\="" 方程式${3^x="5x-1}はの範囲に少なくとも1つの実数解をもつ.}" g(x)=h(x)が実数解をもつことは,\" 閉区間で連続という前提条件を断った上でf(0)とfの異符号を確認し,\="" 中間値の定理を適用する.="" {実数解の具体的な値はわからないが,\="" その存在だけならば容易に示せる}というわけである.="" なお,\="" 初等関数3^xや5xが連続関数であることは明らかとしてよい.\="" その和や差も連続関数であるの範囲に少なくとも1つの実数解をもつ.

