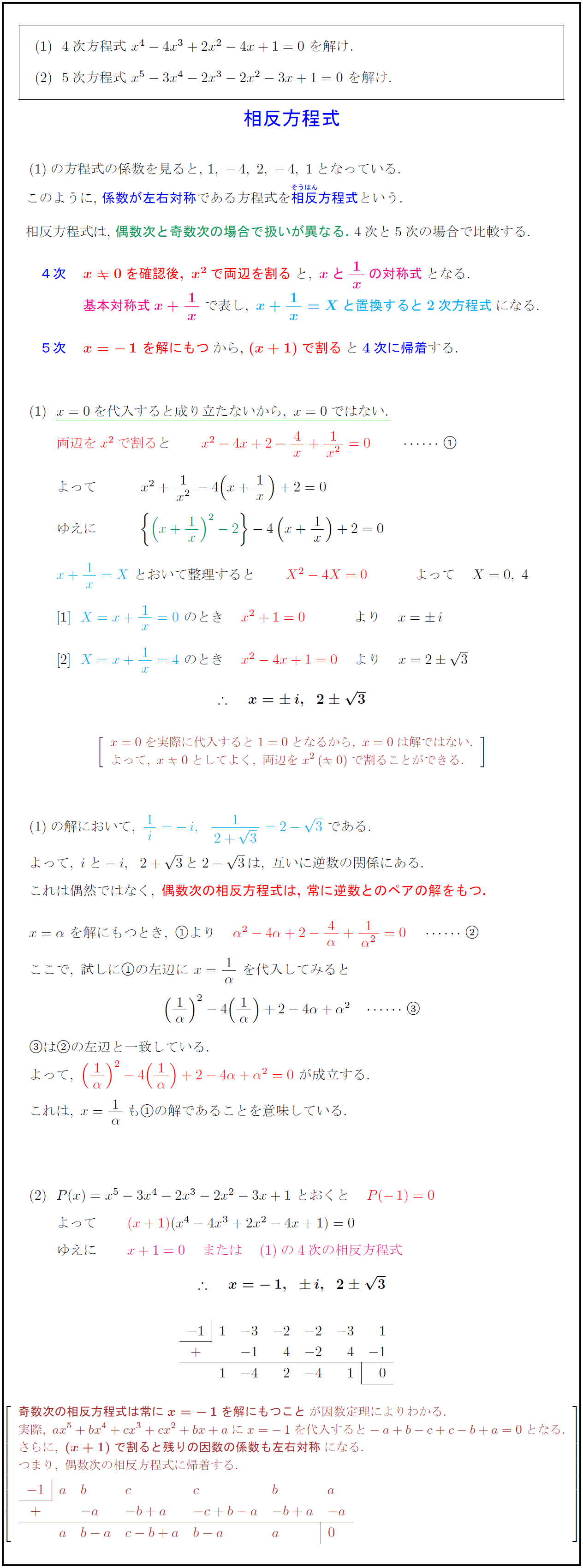
4次方程式\ x^4-4x^3+2x^2-4x+1=0\ を解け.$
$(2)\ \ 5次方程式\ x^5-3x^4-2x^3-2x^2-3x+1=0\ を解け.$ \\
相反方程式}$ \\
(1)の方程式の係数を見ると,\ $1,\ -\,4,\ 2,\ -\,4,\ 1となっている.$
このように,\ 係数が左右対称である方程式を\ruby{相反}{そうはん方程式という.
相反方程式は,偶数次と奇数次の場合で扱いが異なる.\ 4次と5次の場合で比較する.
4次 $x≠0を確認後,\ x^2\,で両辺を割ると,\ xと\,1x\,の対称式となる.$ \\
$基本対称式x+1xで表し,\ x+1x=Xと置換すると2次方程式になる.$
5次 $x=-\,1\ を解にもつ}$}から,\ $(x+1)で割る$と4次に帰着する. {x=0を代入すると成り立たないから,\ x=0ではない.$
$両辺をx^2\,で割る
x=0を実際に代入すると1=0となるから,\ x=0は解ではない.
よって,\ x≠0としてよく,\ 両辺をx^2\,(≠0)で割ることができる.
$(1)の解において,\ 1i=-\,i,\ \ 1}{2+√3}=2-√3}\ である.$
$よって,\ iと-i,\ \ 2+√3\,と2-√3\,は,\ 互いに逆数の関係にある.$
$これは偶然ではなく,\ 偶数次の相反方程式は,\ 常に逆数とのペアの解をもつ.$
$x=α\ を解にもつとき
$ここで,\ 試しに①の左辺に\ x=1}{α}\ を代入してみると$ \
$③は②の左辺と一致している.$成立する.$
$これは,\ x=1}{α}\,も①の解であることを意味している.$ \\
(2)\ \ $P(x)=x^5-3x^4-2x^3-2x^2-3x+1\ とおくと P(-\,1)=0}$
$よって (x+1)}(x^4-4x^3+2x^2-4x+1)=0$
$ゆえに x+1=0 または (1)の4次の相反方程式}$
奇数次の相反方程式は常にx=-\,1を解にもつこと}が因数定理によりわかる.
実際,\ ax^5+bx^4+cx^3+cx^2+bx+aにx=-\,1を代入すると-a+b-c+c-b+a=0となる.
さらに,\ (x+1)で割ると残りの因数の係数も左右対称}になる.
つまり,\ 偶数次の相反方程式に帰着する.

