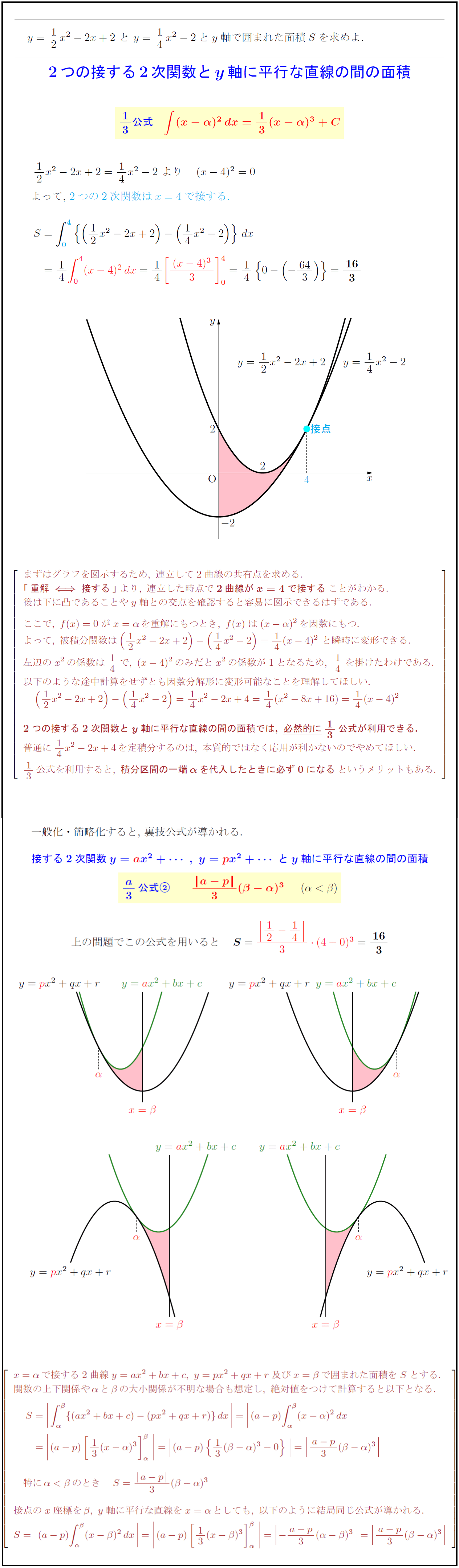
まずはグラフを図示するため,\ 連立して2曲線の共有点を求める.
「\,重解\,⇔\,接する\,」}より,\ 連立した時点で2曲線がx=4で接する}ことがわかる.
後は下に凸であることやy軸との交点を確認すると容易に図示できるはずである.
ここで,\ f(x)=0がx=α\,を重解にもつとき,\ f(x)は(x-α)^2\,を因数にもつ.
よって,\ 被積分関数は12x^2-2x+2-14x^2-2=14(x-4)^2\ と瞬時に変形できる.
左辺のx^2\,の係数は\,14\,で,\ (x-4)^2\,のみだとx^2\,の係数が1となるため,\ 14\,を掛けたわけである.
以下のような途中計算をせずとも因数分解形に変形可能なことを理解してほしい.
2つの接する2次関数とy軸に平行な直線の間の面積では,\ 必然的に}\,13\,公式が利用できる.}
普通に\,14x^2-2x+4\,を定積分するのは,\ 本質的ではなく応用が利かないのでやめてほしい.
13\,公式を利用すると,\ 積分区間の一端\,α\,を代入したときに必ず0になる}というメリットもある.
一般化・簡略化すると,\ 裏技公式が導かれる.
$接する2次関数y=a}x^2+・・・\ ,\ y=p}x^2+・・・\ とy軸に平行な直線の間の面積$}
x=α\,で接する2曲線y=ax^2+bx+c,\ y=px^2+qx+r及びx=β\,で囲まれた面積をSとする.
関数の上下関係や\,α\,と\,β\,の大小関係が不明な場合も想定し,\ 絶対値をつけて計算すると以下となる. \
接点のx座標を\,β,\ y軸に平行な直線をx=α\,としても,\ 以下のように結局同じ公式が導かれる. \

