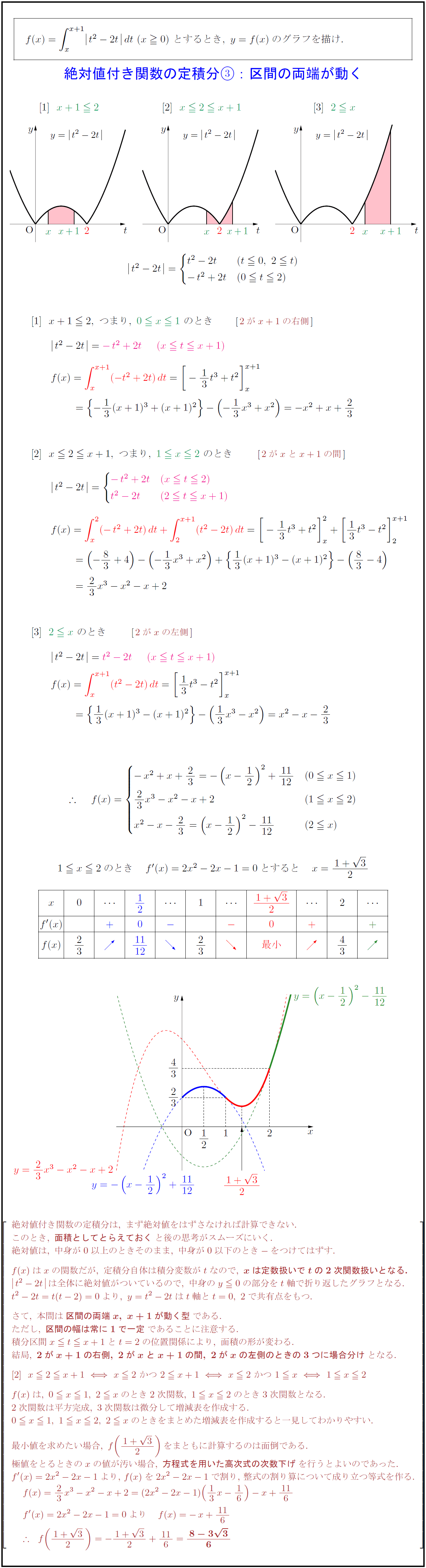
絶対値付き関数の定積分は,\ まず絶対値をはずさなければ計算できない.
このとき,\ 面積としてとらえておく}と後の思考がスムーズにいく.
絶対値は,\ 中身が0以上のときそのまま,\ 中身が0以下のとき-をつけてはずす.
f(x)はxの関数だが,\ 定積分自体は積分変数がtなので,\ xは定数扱いでtの2次関数扱いとなる.}
t^2-2t}\,は全体に絶対値がついているので,\ 中身のy≦0の部分をt軸で折り返したグラフとなる.
t^2-2t=t(t-2)=0より,\ y=t^2-2tはt軸とt=0,\ 2で共有点をもつ.
さて,\ 本問は区間の両端x,\ x+1が動く型}である.
ただし,\ 区間の幅は常に1で一定}であることに注意する.
積分区間x≦ t≦ x+1とt=2の位置関係により,\ 面積の形が変わる.
結局,\ 2がx+1の右側,\ 2がxとx+1の間,\ 2がxの左側のときの3つに場合分け}となる.
f(x)は,\ 0≦ x≦1,\ 2≦ xのとき2次関数,\ 1≦ x≦2のとき3次関数となる.
2次関数は平方完成,\ 3次関数は微分して増減表を作成する.
0≦ x≦1,\ 1≦ x≦2,\ 2≦ xのときをまとめた増減表を作成すると一見してわかりやすい.
最小値を求めたい場合,\ f-.2zw}1+√3}{2}をまともに計算するのは面倒である.
極値をとるときのxの値が汚い場合,\ 方程式を用いた高次式の次数下げ}を行うとよいのであった.
f'(x)=2x^2-2x-1より,\,f(x)を2x^2-2x-1で割り,\,整式の割り算について成り立つ等式を作る.

