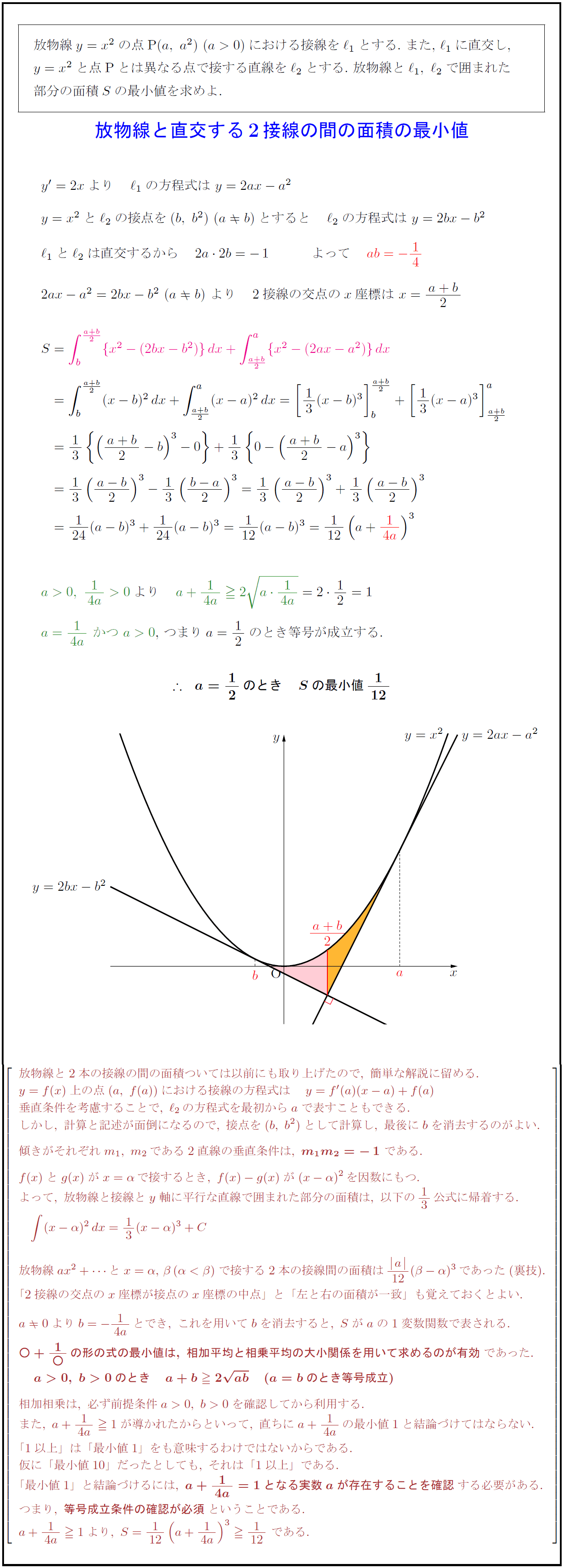
放物線$y=x^2$の点P$(a,\ a^2)\ (a>0)$における接線を$ℓ_1$とする.\ また,\ $ℓ_1$に直交し,
$y=x^2$と点Pとは異なる点で接する直線を$ℓ_2$とする.\ 放物線と$ℓ_1,\ ℓ_2$で囲まれた
部分の面積$S$の最小値を求めよ.放物線と直交する2接線の間の面積の最小値}$}
放物線と2本の接線の間の面積ついては以前にも取り上げたので,\ 簡単な解説に留める.
y=f(x)上の点(a,\ f(a))における接線の方程式は y=f'(a)(x-a)+f(a)
垂直条件を考慮することで,\ ℓ_2\,の方程式を最初からaで表すこともできる.
しかし,\ 計算と記述が面倒になるので,\ 接点を(b,\ b^2)として計算し,\ 最後にbを消去するのがよい.
傾きがそれぞれm_1,\ m_2\,である2直線の垂直条件は,\ m_1m_2=-\,1}\ である.
f(x)とg(x)がx=α\,で接するとき,\ f(x)-g(x)が(x-α)^2\,を因数にもつ.
よって,\ 放物線と接線とy軸に平行な直線で囲まれた部分の面積は,\ 以下の\,13\,公式に帰着する.
∫{}{}(x-α)^2\,dx=13(x-α)^{3}+C
放物線ax^2+・・・ とx=α,\,β\,(α<β)で接する2本の接線間の面積は\, a}{12}(β-α)^3\,であった(裏技).
「2接線の交点のx座標が接点のx座標の中点」と「左と右の面積が一致」も覚えておくとよい.
a≠0よりb=-1}{4a}\,とでき,\ これを用いてbを消去すると,\ Sがaの1変数関数で表される.
○+1}{○}\,の形の式の最小値は,\ 相加平均と相乗平均の大小関係を用いて求めるのが有効}であった.
a>0,\ b>0のとき a+b≧2√{ab} (a=bのとき等号成立)}
相加相乗は,\ 必ず前提条件a>0,\ b>0を確認してから利用する.
また,\ a+1}{4a}≧1が導かれたからといって,\ 直ちにa+1}{4a}\,の最小値1と結論づけてはならない.
「1以上」は「最小値1」をも意味するわけではないからである.
仮に「最小値10」だったとしても,\ それは「1以上」である.
「最小値1」と結論づけるには,\ a+1}{4a}=1となる実数aが存在することを確認}する必要がある.
つまり,\ 等号成立条件の確認が必須}ということである.

