放物線$y=12x^2$と$y$軸上の点を中心とする半径2の円が異なる2点で接しているとき,
放物線と円で囲まれた部分の面積$S$を求めよ.\ ただし,\ 円の内部の面積は含めない. \\
{放物線と円の間の面積}$ \\
円の中心の座標をO$'(0,\ a)$とすると,\ 円の方程式は $x^2+(y-a)^2=4$
$y=12x^2$と連立すると $2y+(y-a)^2=4$
整理すると $y^2-2(a-1)y+a^2-4=0}$
判別式を$D$とすると,\ 円と放物線が異なる2点で接する条件は
$ D4}=\{-\,(a-1)\}^2-(a^2-4)=-\,2a+5=0}$ かつ $a-1>0$
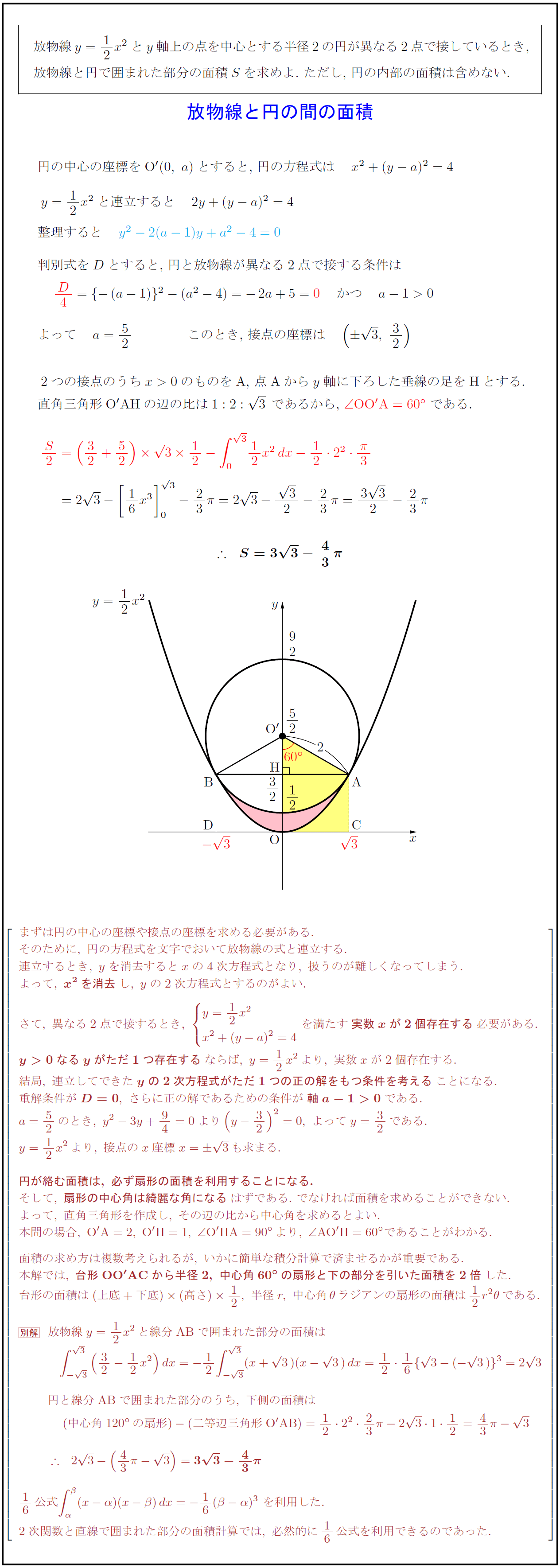
よって $a=52$ このとき,\ 接点の座標は $±√3,\ 32$ \\
2つの接点のうち$x>0$のものをA,\ 点Aから$y$軸に下ろした垂線の足をHとする.
直角三角形$O’AH}の辺の比は1:2:√3\,$であるから,\ $∠OO’A}=60°}$である.
まずは円の中心の座標や接点の座標を求める必要がある.
そのために,\ 円の方程式を文字でおいて放物線の式と連立する.
連立するとき,\ yを消去するとxの4次方程式となり,\ 扱うのが難しくなってしまう.
よって,\ x^2\,を消去}し,\ yの2次方程式とするのがよい.
さて,\ 異なる2点で接するとき,\}を満たす実数xが2個存在する}必要がある. [-1zh]
y>0なるyがただ1つ存在する}ならば,\ y=12x^2\,より,\ 実数xが2個存在する.
結局,\ 連立してできたyの2次方程式がただ1つの正の解をもつ条件を考える}ことになる.
重解条件がD=0},\ さらに正の解であるための条件が軸a-1>0}である.
a=52\,のとき,\ y^2-3y+94=0よりy-32^2=0,\ よってy=32\,である.
y=12x^2\,より,\ 接点のx座標x=±√3\,も求まる.
円が絡む面積は,\ 必ず扇形の面積を利用することになる.}
そして,\ 扇形の中心角は綺麗な角になる}はずである.\ でなければ面積を求めることができない.
よって,\ 直角三角形を作成し,\ その辺の比から中心角を求めるとよい.
本問の場合,\ O’A=2,\ O’H=1,\ ∠ O’HA=90°\,より,\ ∠ AO’H=60°}であることがわかる.
面積の求め方は複数考えられるが,\ いかに簡単な積分計算で済ませるかが重要である.
本解では,\ 台形OO’AC}から半径2,\ 中心角60°\,の扇形と下の部分を引いた面積を2倍}した.
台形の面積は(上底+下底)×(高さ)×12,\ 半径r,\ 中心角\,θ\,ラジアンの扇形の面積は\,12r^2θ\,である.
放物線y=12x^2\,と線分AB}で囲まれた部分の面積は
}円と線分AB}で囲まれた部分のうち,\ 下側の面積は
} (中心角120°\,の扇形)-(二等辺三角形 を利用した.
2次関数と直線で囲まれた部分の面積計算では,\ 必然的に\,16\,公式を利用できるのであった.

