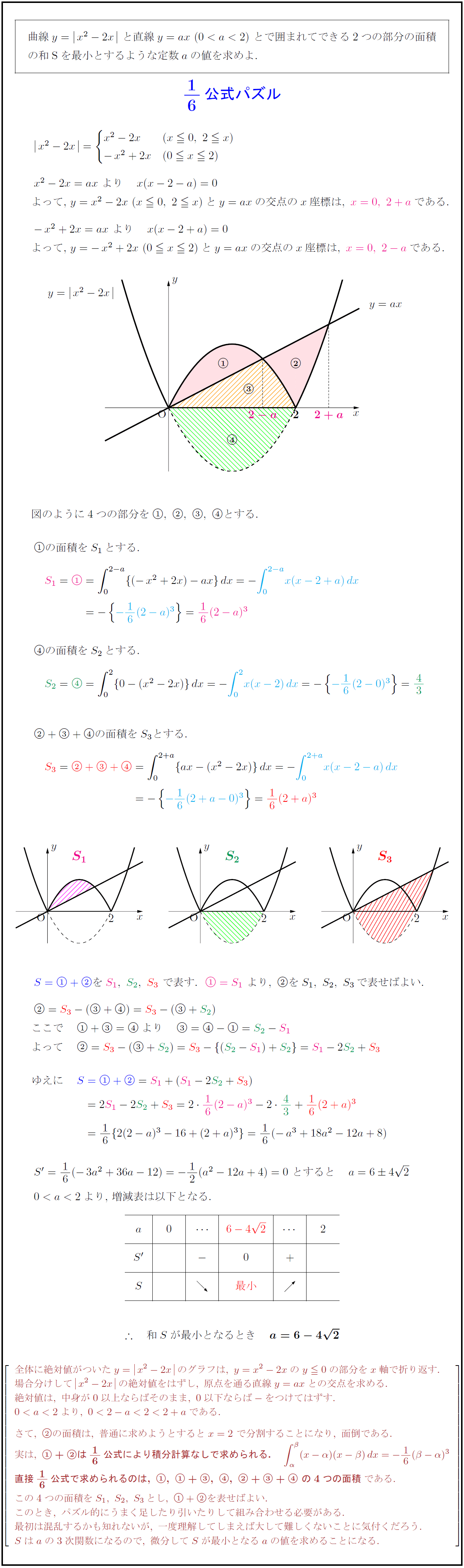
全体に絶対値がついたy=x^2-2x}\,のグラフは,\ y=x^2-2xのy≦0の部分をx軸で折り返す.
場合分けして\,x^2-2x}\,の絶対値をはずし,\ 原点を通る直線y=axとの交点を求める.
絶対値は,\ 中身が0以上ならばそのまま,\ 0以下ならば-をつけてはずす.
さて,\ ②の面積は,\ 普通に求めようとするとx=2\ で分割することになり,\ 面倒である.
実は,\ ①+②は\,16\,公式により積分計算なしで求められる.} ∫{α}{β}(x-α)(x-β)\,dx=-16(β-α)^3
直接\,16\,公式で求められるのは,\ ①,\ ①+③,\ ④,\ ②+③+④\ の4つの面積}である.
この4つの面積をS_1,\ S_2,\ S_3\,とし,\ ①+②を表せばよい.
このとき,\ パズル的にうまく足したり引いたりして組み合わせる必要がある.
最初は混乱するかも知れないが,\ 一度理解してしまえば大して難しくないことに気付くだろう.
Sはaの3次関数になるので,\ 微分してSが最小となるaの値を求めることになる.

