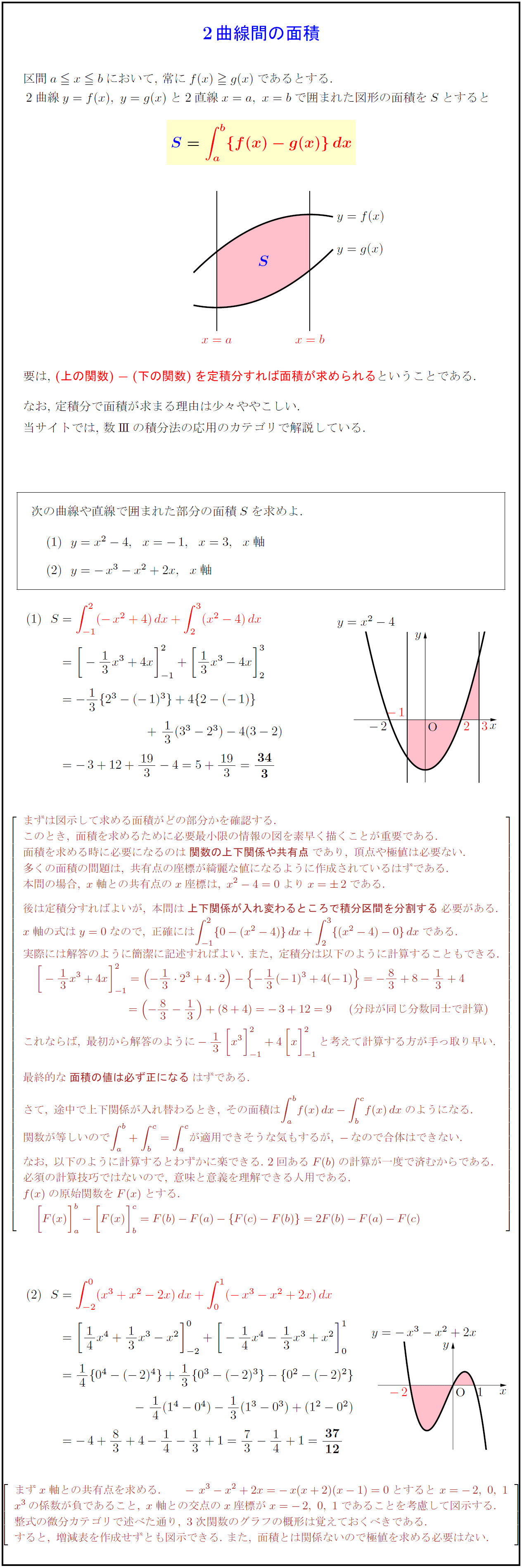
区間$a≦ x≦ b$において,\ 常に$f(x)≧ g(x)$であるとする. \\
2曲線$y=f(x),\ y=g(x)$と2直線$x=a,\ x=b$で囲まれた図形の面積を$S$とすると
要は,\$(上の関数)-(下の関数)}$を定積分すれば面積が求められるということである.
なお,\ 定積分で面積が求まる理由は少々ややこしい.
当サイトでは,\ 数IIIの積分法の応用のカテゴリで解説している. \\
次の曲線や直線で囲まれた部分の面積$S$を求めよ.
まずは図示して求める面積がどの部分かを確認する.
このとき,\ 面積を求めるために必要最小限の情報の図を素早く描くことが重要である.
面積を求める時に必要になるのは関数の上下関係や共有点}であり,\ 頂点や極値は必要ない.
多くの面積の問題は,\ 共有点の座標が綺麗な値になるように作成されているはずである.
本問の場合,\ x軸との共有点のx座標は,\ x^2-4=0よりx=±\,2である.
後は定積分すればよいが,\ 本問は上下関係が入れ変わるところで積分区間を分割する}必要がある.
x軸の式はy=0なので,\ 正確には∫{-1}{2}\{0-(x^2-4)\}\,dx+∫{2}{3}\{(x^2-4)-0\}\,dxである.
実際には解答のように簡潔に記述すればよい.\ また,\ 定積分は以下のように計算することもできる.(分母が同じ分数同士で計算)
これならば,\ 最初から解答のように-13[x^3}{-1}{2}+4[x}{-1}{2}と考えて計算する方が手っ取り早い.
最終的な面積の値は必ず正になる}はずである.
さて,\ 途中で上下関係が入れ替わるとき,\ その面積は∫{a}{b}f(x)\,dx-∫{b}{c}f(x)\,dxのようになる.
関数が等しいので∫{a}{b}+∫{b}{c}=∫{a}{c}が適用できそうな気もするが,\ -\,なので合体はできない.
なお,\ 以下のように計算するとわずかに楽できる.\ 2回あるF(b)の計算が一度で済むからである.
必須の計算技巧ではないので,\ 意味と意義を理解できる人用である.
f(x)の原始関数をF(x)とする.
[F(x)}{a}{b}-[F(x)}{b}{c}=F(b)-F(a)-\{F(c)-F(b)\}=2F(b)-F(a)-F(c)
まずx軸との共有点を求める. -\,x^3-x^2+2x=-\,x(x+2)(x-1)=0とすると\ x=-\,2,\ 0,\ 1
x^3\,の係数が負であること,\ x軸との交点のx座標がx=-\,2,\ 0,\ 1であることを考慮して図示する.
整式の微分カテゴリで述べた通り,\ 3次関数のグラフの概形は覚えておくべきである.
すると,\ 増減表を作成せずとも図示できる.\ また,\ 面積とは関係ないので極値を求める必要はない.

