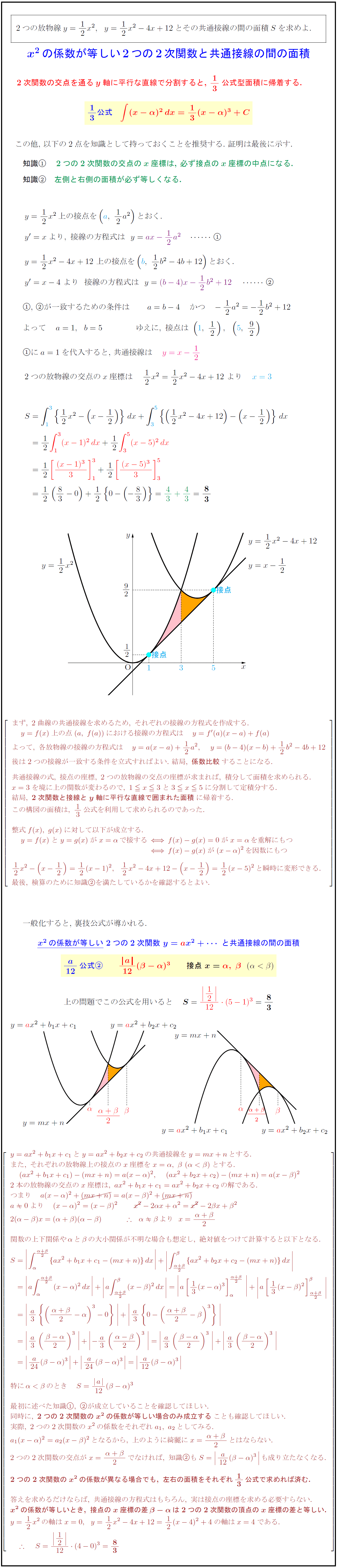
2次関数の交点を通る$y}$軸に平行な直線で分割すると,\ $13}$公式型面積に帰着する.
この他,\ 以下の2点を知識として持っておくことを推奨する.\ 証明は最後に示す.
知識① {2つの2次関数の交点の$x}$座標は,\ 必ず接点の$x}$座標の中点になる.
知識② \{左側と右側の面積が必ず等しくなる.
まず,\ 2曲線の共通接線を求めるため,\ それぞれの接線の方程式を作成する.
y=f(x)上の点(a,\ f(a))における接線の方程式は y=f'(a)(x-a)+f(a)
よって,\ 各放物線の接線の方程式は y=a(x-a)+12a^2, y=(b-4)(x-b)+12b^2-4b+12
後は2つの接線が一致する条件を立式すればよい.\ 結局,\ 係数比較}することになる.
共通接線の式,\ 接点の座標,\ 2つの放物線の交点の座標が求まれば,\ 積分して面積を求められる.
x=3を境に上の関数が変わるので,\ 1≦ x≦3と3≦ x≦5に分割して定積分する.
結局,\ 2次関数と接線とy軸に平行な直線で囲まれた面積}に帰着する.
この構図の面積は,\ 13\,公式を利用して求められるのであった.
整式f(x),\ g(x)に対して以下が成立する.
y=f(x)とy=g(x)がx=α\,で接する\,⇔\,f(x)-g(x)=0がx=α\,を重解にもつ
y=f(x)とy=g(x)がx=α\,で接する}\,⇔\,f(x)-g(x)が(x-α)^2\,を因数にもつ
12x^2-x-12=12(x-1)^2,\ \ 12x^2-4x+12-x-12=12(x-5)^2\,と瞬時に変形できる.
最後,\ 検算のために知識②を満たしているかを確認するとよい.
一般化すると,\ 裏技公式が導かれる.
$x^2\,の係数が等しい}\ 2つの2次関数\ y=a}x^2+・・・\ と共通接線の間の面積
y=ax^2+b_1x+c_1\,とy=ax^2+b_2x+c_2\,の共通接線をy=mx+n\,とする.
また,\ それぞれの放物線上の接点のx座標をx=α,\ β\ (α<β)とする.
(ax^2+b_1x+c_1)-(mx+n)=a(x-α)^2, (ax^2+b_2x+c_2)-(mx+n)=a(x-β)^2
2本の放物線の交点のx座標は,\ ax^2+b_1x+c_1=ax^2+b_2x+c_2\,の解である.
つまり a(x-α)^2+\teisei{(mx+n)}=a(x-β)^2+\teisei{(mx+n)}
a≠0より (x-α)^2=(x-β)^2 \teisei{x^2}-2α x+α^2=\teisei{x^2}-2β x+β^2
2(α-β)x=(α+β)(α-β) ∴\ \ α≠β\,より\ \ x=α+β}{2}
関数の上下関係や\,α\,と\,β\,の大小関係が不明な場合も想定し,\ 絶対値をつけて計算すると以下となる.
最初に述べた知識①,\ ②が成立していることを確認してほしい.
同時に,\ 2つの2次関数のx^2\,の係数が等しい場合のみ成立する}ことも確認してほしい.
実際,\ 2つの2次関数のx^2\,の係数をそれぞれa_1,\ a_2\,としてみる.
a_1(x-α)^2=a_2(x-β)^2\,となるから,\ 上のように綺麗にx=α+β}{2}\,とはならない.
2つの2次関数の交点がx=α+β}{2}\,でなければ,\ 知識②もS=a\vphantom b}{12}(β-α)^3}\,も成り立たなくなる.
2つの2次関数のx^2\,の係数が異なる場合でも,\ 左右の面積をそれぞれ\,13\,公式で求めれば済む.}
答えを求めるだけならば,\ 共通接線の方程式はもちろん,\ 実は接点の座標を求める必要すらない.
x^2\,の係数が等しいとき,\ 接点のx座標の差\,β-α\,は2つの2次関数の頂点のx座標の差と等しい.} \\

