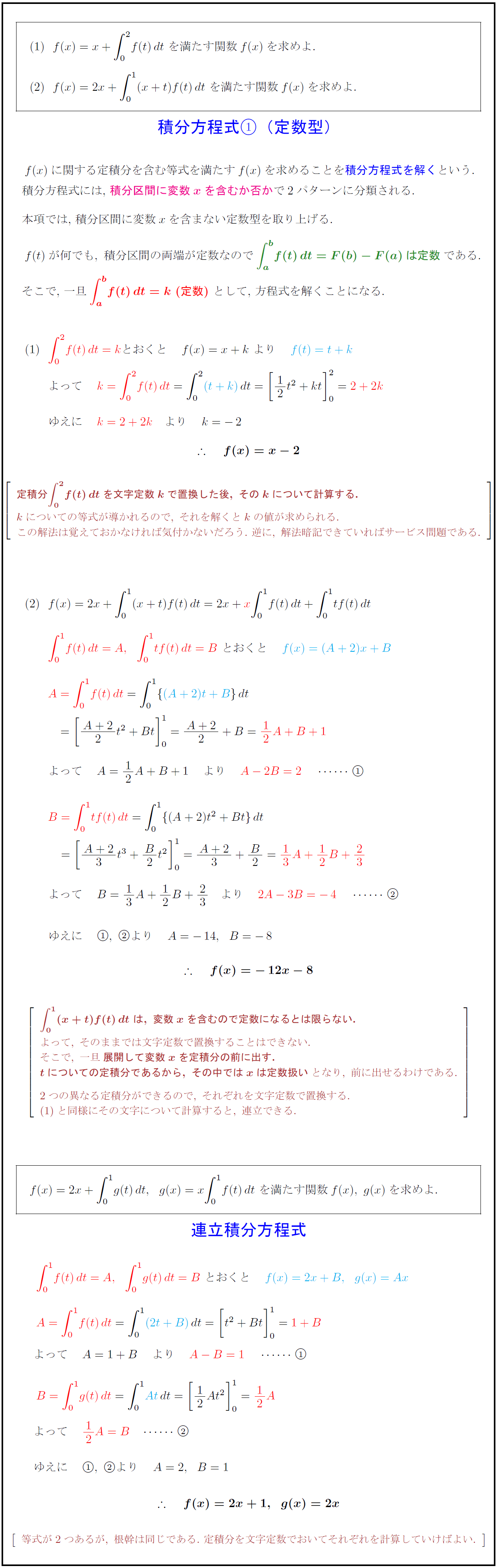
$f(x)=x+∫{0}{2}f(t)\,dt\ を満たす関数f(x)を求めよ.$
(2)\ \ $f(x)=2x+∫{0}{1}(x+t)f(t)\,dt\ を満たす関数f(x)を求めよ.$ \\
{積分方程式①(定数型) \\
$f(x)$に関する定積分を含む等式を満たす$f(x)$を求めることを積分方程式を解くという.
積分方程式には,\ 積分区間に変数$x}$を含むか否かで2パターンに分類される.
本項では,\ 積分区間に変数$x$を含まない定数型を取り上げる.
$f(t)が何でも,\ 積分区間の両端が定数なので∫{a}{b}f(t)\,dt=F(b)-F(a)は定数である.$
そこで,\ 一旦$∫{a}{b}f(t)\,dt=k\ (定数)$\ として,\ 方程式を解くことになる.
定積分∫{0}{2}f(t)\,dtを文字定数kで置換した後,\ そのkについて計算する.}
kについての等式が導かれるので,\ それを解くとkの値が求められる.
この解法は覚えておかなければ気付かないだろう.\ 逆に,\ 解法暗記できていればサービス問題である
∫{0}{1}(x+t)f(t)\,dt\ は,\ 変数xを含むので定数になるとは限らない.}
よって,\ そのままでは文字定数で置換することはできない.
そこで,\ 一旦展開して変数xを定積分の前に出す.}
tについての定積分であるから,\ その中ではxは定数扱い}となり,\ 前に出せるわけである.
2つの異なる定積分ができるので,\ それぞれを文字定数で置換する.
(1)と同様にその文字について計算すると,\ 連立できる.
等式が2つあるが,\ 根幹は同じである.\ 定積分を文字定数でおいてそれぞれを計算していけばよい.

