3次関数$y=x^3-6x^2+9x$と直線$y=mx$が$x≧0$において異なる3点で交わ
\ \ るような$m$の値の範囲を求めよ.
(2)\ \ (1)のとき,\ 3次関数と直線で囲まれてできる2つの部分の面積を等しくするよう
\ \ な定数$m$の値を求めよ. \\
等積条件の工夫③ $S_1-S_2=0}$ \\
$定積分の性質を利用するため,\ S_1=S_2\ ⇔\ S_1-S_2=0$\ と考える.
(1)\ \ $x^3-6x^2+9x=mx\ より x\{x^2-6x+(9-m)\}=0$
よって $x=0\ \ または\ \ x^2-6x+(9-m)=0\ (①)}$
①が異なる2個の正の解をもてば,\ 3次関数と直線が$x≧0$の異なる3点で交わる.
連立すると因数分解でき,\ x=0を必ず解にもつことがわかる.
よって,\ 2次方程式①が異なる2個の正の解をもてばよい.
結局,\ 数 Iで学習した解の存在範囲(配置)の問題}となる.
これは,\ グラフを用いて図形的に考えるのであった.
つまり,\ 2次関数f(x)=x^2-6x+(9-m)がx軸の正の部分と異なる2点で交わればよい.}
その条件は D>0,\ \ 軸>0,\ \ f(0)>0}
f(x)=(x-3)^2-mより軸は常にx=3>0なので,\ D>0とf(0)>0を考慮すれば済む. \\[-15zh]
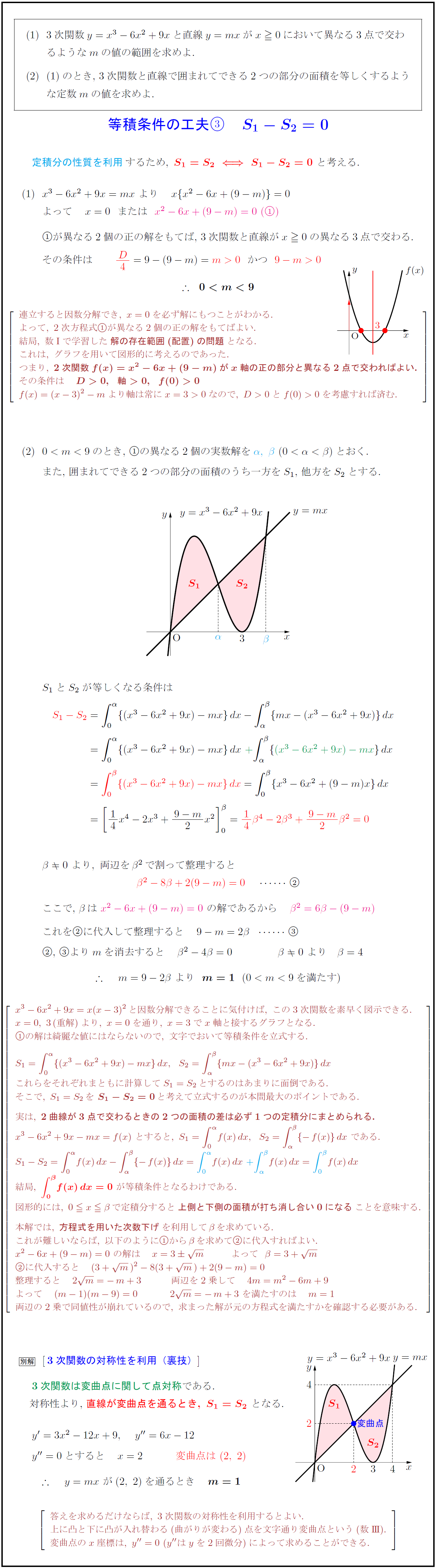
①の異なる2個の実数解を$α,\ β}\ (0<α<β)$とおく.
また,\ 囲まれてできる2つの部分の面積のうち一方を$S_1$,\ 他方を$S_2$とする. \\\ $β≠0\ より,\ 両辺を\,β^2\,で割って整理すると$
x^3-6x^2+9x=x(x-3)^2\,と因数分解できることに気付けば,\ この3次関数を素早く図示できる.
x=0,\ 3\,(重解)より,\ x=0を通り,\ x=3でx軸と接するグラフとなる.
①の解は綺麗な値にはならないので,\ 文字でおいて等積条件を立式する.
これらをそれぞれまともに計算してS_1=S_2\,とするのはあまりに面倒である.
そこで,\ S_1=S_2\,を\ S_1-S_2=0}\,と考えて立式するのが本問最大のポイントである.
実は,\ 2曲線が3点で交わるときの2つの面積の差は必ず1つの定積分にまとめられる.}
結局,\ ∫{0}{β}f(x)\,dx=0\ が等積条件となるわけである.
図形的には,\ 0≦ x≦β\,で定積分すると上側と下側の面積が打ち消し合い0になる}ことを意味する.
本解では,\ 方程式を用いた次数下げ}を利用して\,β\,を求めている.
これが難しいならば,\ 以下のように①から\,β\,を求めて②に代入すればよい. \\
両辺の2乗で同値性が崩れているので,\ 求まった解が元の方程式を満たすかを確認する必要がある.
\,3次関数の対称性を利用(裏技)]3次関数は変曲点に関して点対称である.
対称性より,\ $直線が変曲点を通るとき,\ S_1=S_2$\ となる.
答えを求めるだけならば,\ 3次関数の対称性を利用するとよい.
上に凸と下に凸が入れ替わる(曲がりが変わる)点を文字通り変曲点という(数
変曲点のx座標は,\ y''=0\ (y''はyを2回微分)によって求めることができる.

