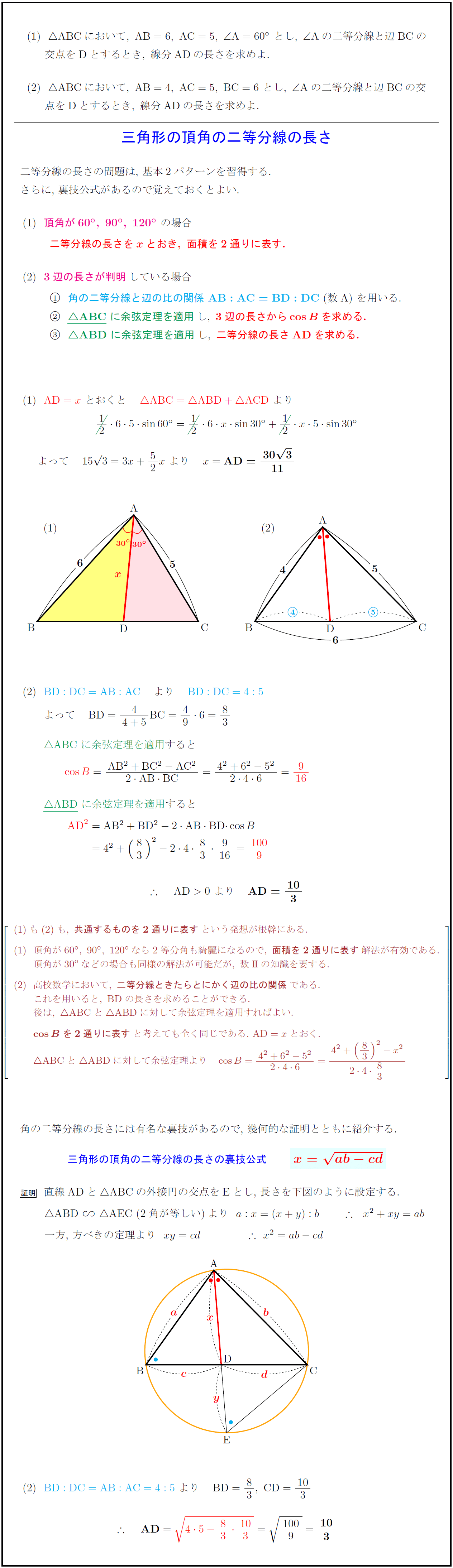
ABCにおいて,\ AB=6,\ AC=5,\ ∠ A=60°\ とし,\ ∠ Aの二等分線と辺BCの}$ $\ {交点をDとするとき,\ 線分ADの長さを求めよ.}$ ${ ABCにおいて,\ AB=4,\ AC=5,\ BC=6\ とし,\ ∠ Aの二等分線と辺BCの交}$ $\ {点をDとするとき,\ 線分ADの長さを求めよ.}$ 三角形の頂角の二等分線の長さ 二等分線の長さの問題は,\ 基本2パターンを習得する. さらに,\ 裏技公式があるので覚えておくとよい. \}{頂角が60°,\ 90°,\ 120°\ の場合$ { } ${二等分線の長さをxとおき,\ 面積を2通りに表す.$ ${3辺の長さが判明している場合$ { } ${角の二等分線と辺の比の関係\ {AB:AC=BD:DC}\ (数 A)\ を用いる.$ に余弦定理を適用し,\ {3辺の長さからcos Bを求める.$ に余弦定理を適用し,\ {二等分線の長さ{AD}を求める.$ もも,\ {共通するものを2通りに表す}という発想が根幹にある. 頂角が60°,\ 90°,\ 120°なら2等分角も綺麗になるので,\ {面積を2通りに表す}解法が有効である. 頂角が30°などの場合も同様の解法が可能だが,\ 数II}の知識を要する. 高校数学において,\ {二等分線ときたらとにかく辺の比の関係}である. これを用いると,\ {BD}の長さを求めることができる. 後は,\ { ABCと ABD}に対して余弦定理を適用すればよい. {cos Bを2通りに表す}と考えても全く同じである.\ {AD}=xとおく. [0zh] { ABCと ABD}に対して余弦定理より 角の二等分線の長さには有名な裏技}があるので,\ 幾何的な証明とともに紹介する. ${三角形の頂角の二等分線の長さの裏技公式$ {n{ab-cd}$} 直線ADと$$ABCの外接円の交点をEとし,\ 長さを下図のように設定する. \ ${ABD∽ AEC}$\ (2角が等しい)より$a:x=(x+y):b$ $x²+xy=ab$ \ 一方,\ 方べきの定理より$xy=cd$ $$ $x²=ab-cd$

