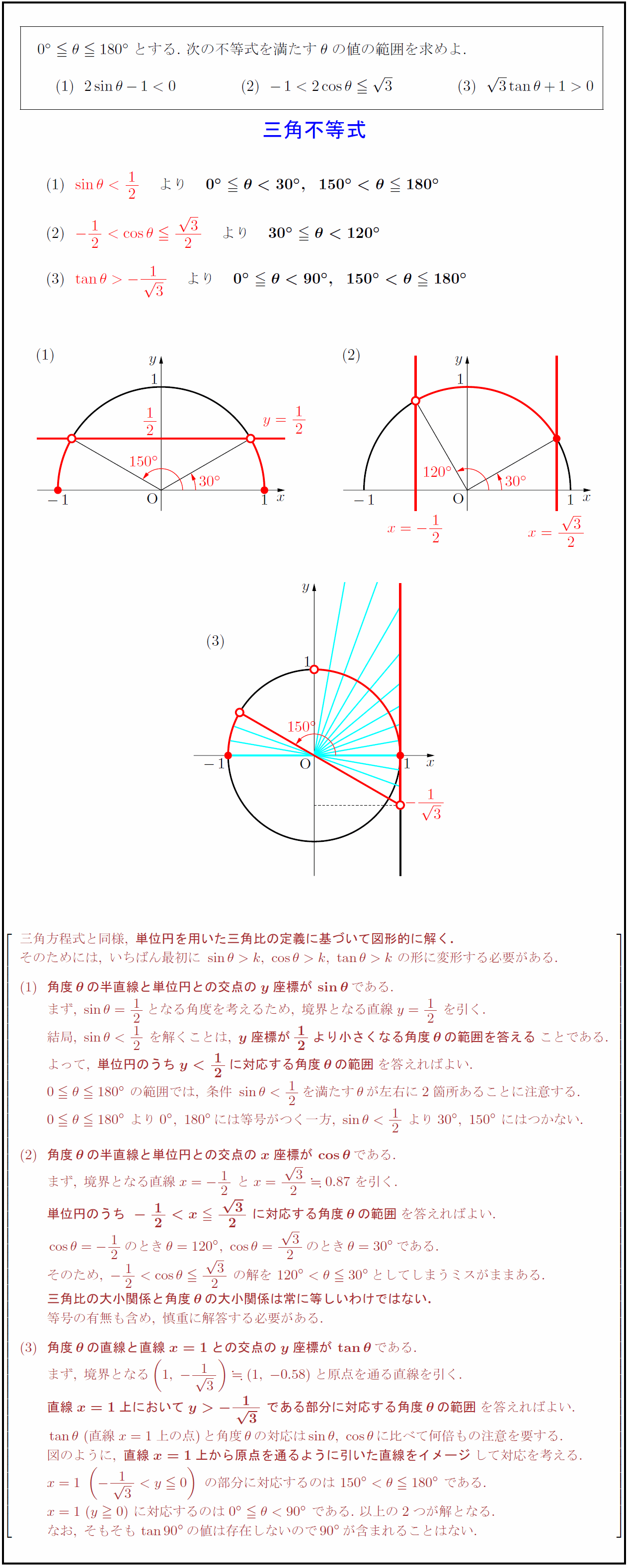
とする.\ 次の不等式を満たす$θ$の値の範囲を求めよ. 三角方程式と同様,\ {単位円を用いた三角比の定義に基づいて図形的に解く.} そのためには,\ いちばん最初に\ sinθ>k,\ cosθ>k,\ tanθ>k\ の形に変形する必要がある. {角度θの半直線と単位円との交点のy座標がsinθ}である. まず,\ sinθ=12となる角度を考えるため,\ 境界となる直線y=12\ を引く. 結局,\ sinθ<12\ を解くことは,\ {y座標が12より小さくなる角度θの範囲を答える}ことである. よって,\ {単位円のうちy<12に対応する角度θの範囲}を答えればよい. 0θ180°\ の範囲では,\ 条件\ sinθ<12を満たすθが左右に2箇所あることに注意する. 0θ180°\ より0°,\ 180°には等号がつく一方,\ sinθ<12\ より30°,\ 150°\ にはつかない. {角度θの半直線と単位円との交点のx座標がcosθ}である. まず,\ 境界となる直線x=-12\ とx={3}{2}0.87\ を引く. {単位円のうち}\ に対応する角度θの範囲}を答えればよい.=”” の解を\=°としてしまうミスがままある.=”” {三角比の大小関係と角度θの大小関係は常に等しいわけではない.}=”” 等号の有無も含め,\=”” 慎重に解答する必要がある.=”” {角度θの直線と直線x=”1との交点のy座標がtanθ}である.” まず,\=”” 境界となる(1,\=”” -{1}{3})(1,\=”” -0.58)と原点を通る直線を引く.=”” {直線x=”1上においてy-{1}{3}\ である部分に対応する角度θの範囲}を答えればよい. tanθ\ (直線x=1上の点)と角度θの対応はsinθ,\ cosθに比べて何倍もの注意を要する. 図のように,\ {直線x=1上から原点を通るように引いた直線をイメージ}して対応を考える” である.\=”” 以上の2つが解となる.=”” なお,\=”” そもそもtan90°の値は存在しないので90°が含まれることはない.

