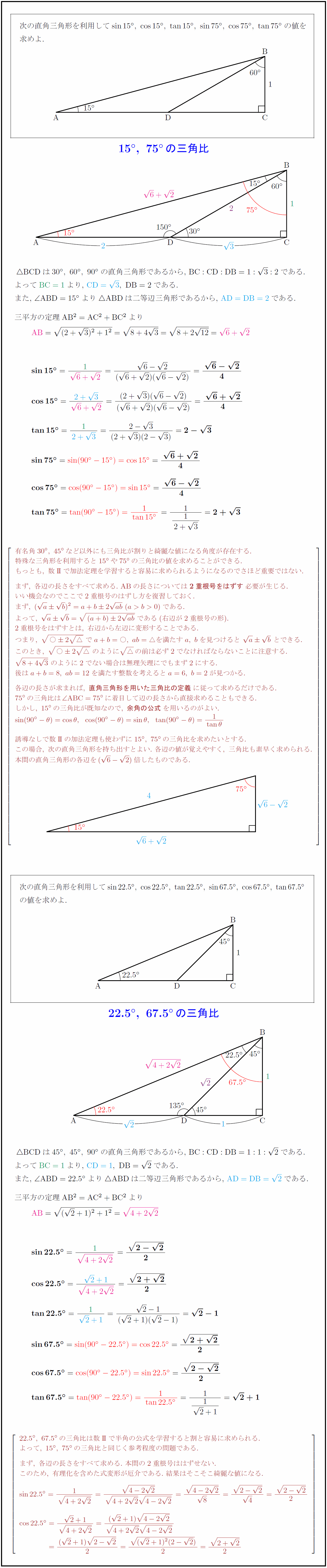
次の直角三角形を利用して$sin15°,\ cos15°,\ tan15°,\ sin75°,\ cos75°,\ tan75°$の値を の直角三角形であるから,\ ${BC:CD:DB=1:3:2}$である. また,\ $∠{ABD}=15°$より$$ABDは二等辺三角形であるから,\ ${AD=DB}=2}$である. 三平方の定理 有名角30°,\ 45°など以外にも三角比が割りと綺麗な値になる角度が存在する. 特殊な三角形を利用すると15°や75°の三角比の値を求めることができる. もっとも,\ 数II}で加法定理を学習すると容易に求められるようになるのでさほど重要ではない. まず,\ 各辺の長さをすべて求める.\ {AB}の長さについては{2重根号をはずす}必要が生じる. いい機会なのでここで2重根号のはずし方を復習しておく. (a+b)2{ab}\ である(右辺が2重根号の形). 2重根号をはずすとは,\ 右辺から左辺に変形することである. つまり,\ a} }-5zw}○2{△ab\ でa+b=○,\ ab=△を満たすa,\ bを見つけると\ a b\ とできる. このとき,\ a} }-5zw}○2{△ab\ のように{△}の前は必ず2でなければならないことに注意する. {8+43}\ のように2でない場合は無理矢理にでもまず2にする. 後はa+b=8,\ ab=12を満たす整数を考えるとa=6,\ b=2が見つかる. 各辺の長さが求まれば,\ {直角三角形を用いた三角比の定義}に従って求めるだけである. 75°の三角比は∠{ABC}=75°に着目して辺の長さから直接求めることもできる. しかし,\ 15°の三角比が既知なので,\ {余角の公式}を用いるのがよい. 誘導なしで数II}の加法定理も使わずに15°,\ 75°の三角比を求めたいとする. この場合,\ 次の直角三角形を持ち出すとよい.\ 各辺の値が覚えやすく,\ 三角比も素早く求められる. 本問の直角三角形の各辺を(6-2)倍したものである. $$BCDは$45°,\ 45°,\ 90°$の直角三角形であるから,\ ${BC:CD:DB=1:1:2}$である. よって${BC}=1}$より,\ ${CD=1},\ DB=2}$である. また,\ $∠{ABD}=22.5°$より$$ABDは二等辺三角形であるから,\ ${AD=DB}=2}$である. 三平方の定理 22.5°,\ 67.5°の三角比は数II}で半角の公式を学習すると割と容易に求められる. よって,\ 15°,\ 75°の三角比と同じく参考程度の問題である. まず,\ 各辺の長さをすべて求める.\ 本問の2重根号ははずせない. このため,\ 有理化を含めた式変形が厄介である.\ 結果はそこそこ綺麗な値になる.

