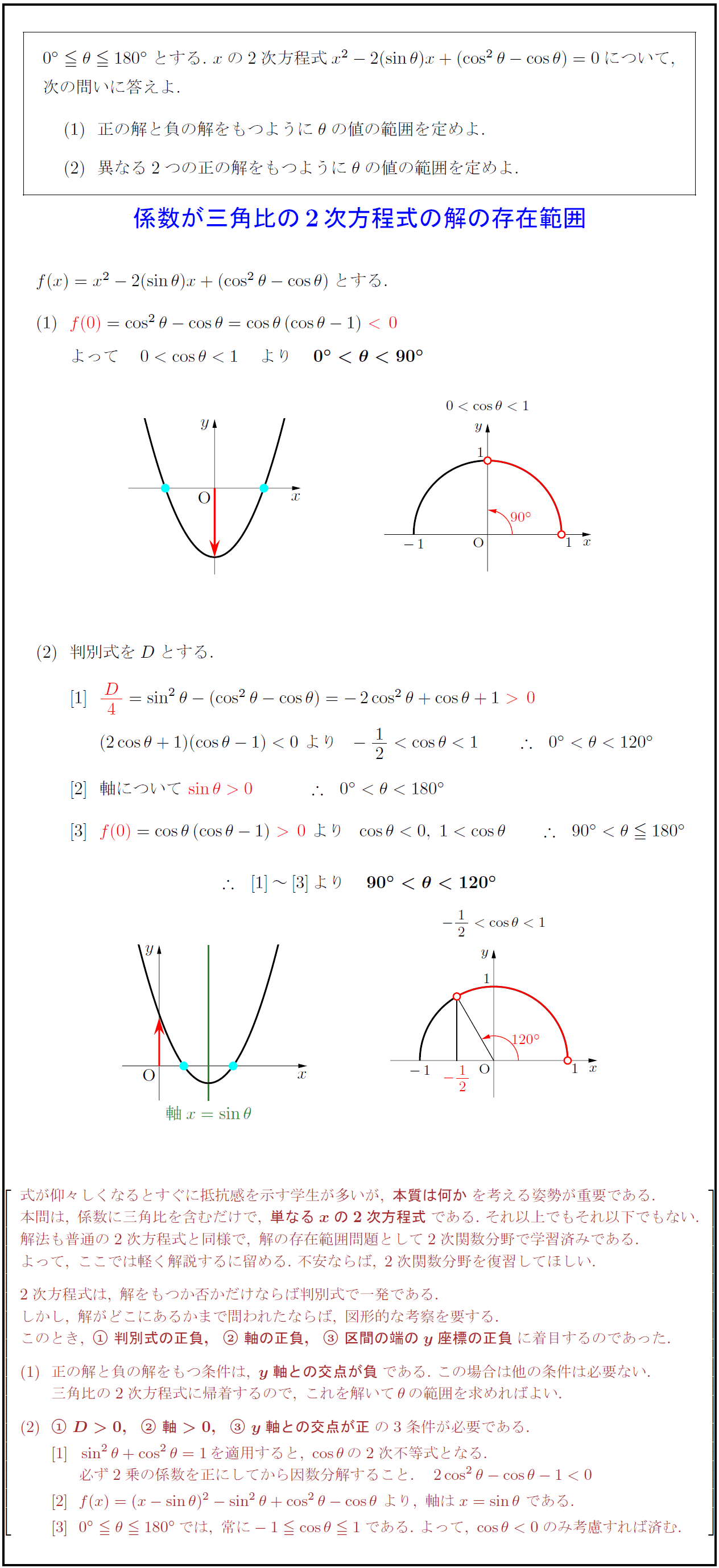
0°θ180°$とする.\ $x$の2次方程式$x²-2(sinθ)x+(cos²θ-cosθ)=0$について, 次の問いに答えよ. 正の解と負の解をもつように$θ$の値の範囲を定めよ. 異なる2つの正の解をもつように$θ$の値の範囲を定めよ. 係数が三角比の2次方程式の解の存在範囲 式が仰々しくなるとすぐに抵抗感を示す学生が多いが,\ {本質は何か}を考える姿勢が重要である. 本問は,\ 係数に三角比を含むだけで,\ {単なるxの2次方程式}である.\ それ以上でもそれ以下でもない. 解法も普通の2次方程式と同様で,\ 解の存在範囲問題として2次関数分野で学習済みである. よって,\ ここでは軽く解説するに留める.\ 不安ならば,\ 2次関数分野を復習してほしい. 2次方程式は,\ 解をもつか否かだけならば判別式で一発である. しかし,\ 解がどこにあるかまで問われたならば,\ 図形的な考察を要する. このとき,\ {\ 判別式の正負,\ 軸の正負,\ 区間の端のy座標の正負}に着目するのであった. 正の解と負の解をもつ条件は,\ {y軸との交点が負}である.\ この場合は他の条件は必要ない. 三角比の2次方程式に帰着するので,\ これを解いてθの範囲を求めればよい. {\ D>0,\ 軸>0,\ y軸との交点が正}の3条件が必要である. sin²θ+cos²θ=1を適用すると,\ cosθの2次不等式となる. 必ず2乗の係数を正にしてから因数分解すること. 2cos²θ-cosθ-1<0 f(x)=(x-sinθ)²-sin²θ+cos²θ-cosθ\ より,\ 軸はx=sinθ\ である. [3]0°θ180°では,\ 常に-1cosθ1である.\ よって,\ cosθ<0のみ考慮すれば済む.

