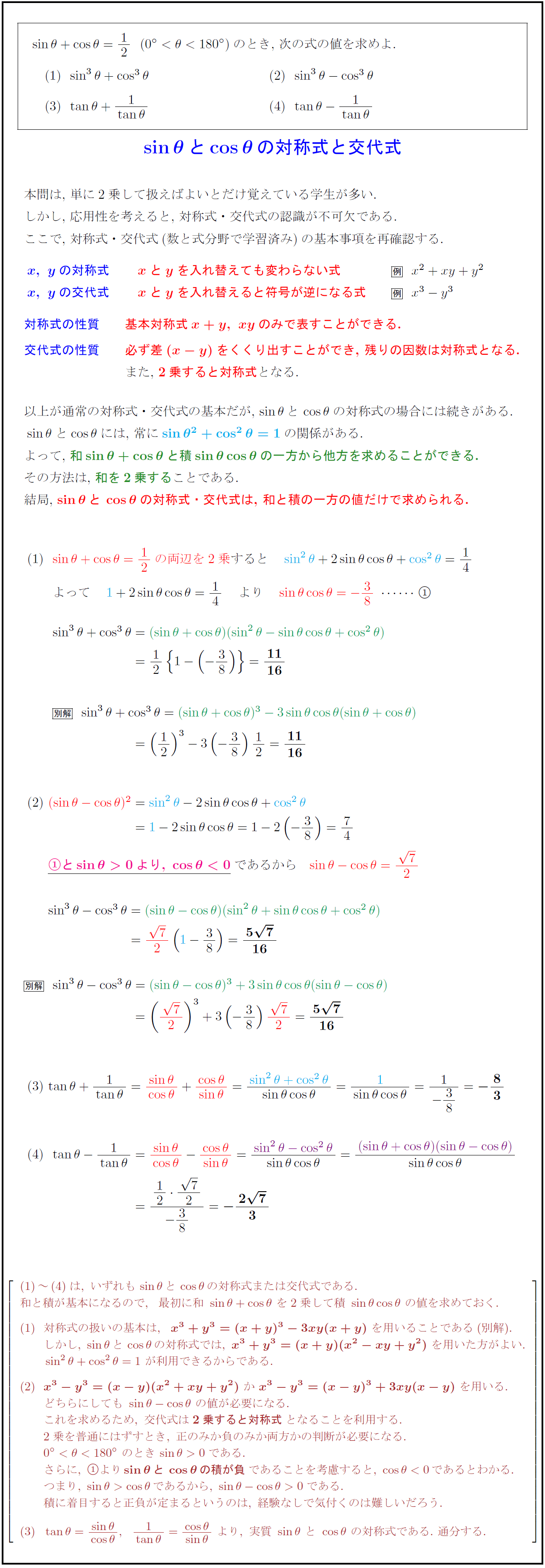
の対称式と交代式 本問は,\ 単に2乗して扱えばよいとだけ覚えている学生が多い. しかし,\ 応用性を考えると,\ 対称式・交代式の認識が不可欠である. ここで,\ 対称式・交代式(数と式分野で学習済み)の基本事項を再確認する. ${x,\ y}$の対称式 ${x}$と${y}$を入れ替えても変わらない式 $x²+xy+y²$ ${x,\ y}$の交代式 ${x}$と${y}$を入れ替えると符号が逆になる式 $x³-y³$ 対称式の性質 基本対称式${x+y,\ xy}$のみで表すことができる. 交代式の性質 必ず差${(x-y)}$をくくり出すことができ,\ 残りの因数は対称式となる. また,\ 2乗すると対称式となる. 以上が通常の対称式・交代式の基本だが,\ $sinθとcosθ$の対称式の場合には続きがある. $sinθ$と$cosθ$には,\ 常に${sinθ²+cos²θ=1$の関係がある. よって,\ 和${sinθ+cosθ}$と積${sinθcosθ}$の一方から他方を求めることができる. その方法は,\ 和を2乗することである. 結局,\ ${sinθとcosθ}$の対称式・交代式は,\ 和と積の一方の値だけで求められる. ~は,\ いずれもsinθとcosθの対称式または交代式である. 和と積が基本になるので,最初に和\ sinθ+cosθ\ を2乗して積\ sinθcosθ\ の値を求めておく. 対称式の扱いの基本は,{x³+y³=(x+y)³-3xy(x+y)}\ を用いることである(別解). しかし,\ sinθとcosθの対称式では,\ {x³+y³=(x+y)(x²-xy+y²)}\ を用いた方がよい. sin²θ+cos²θ=1\ が利用できるからである. {x³-y³=(x-y)(x²+xy+y²)}\ か\ {x³-y³=(x-y)³+3xy(x-y)}\ を用いる. どちらにしても\ sinθ-cosθ\ の値が必要になる. これを求めるため,\ 交代式は{2乗すると対称式}となることを利用する. 2乗を普通にはずすとき,\ 正のみか負のみか両方かの判断が必要になる. 0°<θ<180°\ のときsinθ>0である. さらに,\ より{sinθとcosθの積が負}であることを考慮すると,\ cosθ<0であるとわかる. つまり,\ sinθ>cosθであるから,\ sinθ-cosθ>0である. 積に着目すると正負が定まるというのは,\ 経験なしで気付くのは難しいだろう. tanθ={sinθ}{cosθ},{1}{tanθ}={cosθ}{sinθ}\ より,\ 実質\ sinθ\ と\ cosθ\ の対称式である.\ 通分する.

