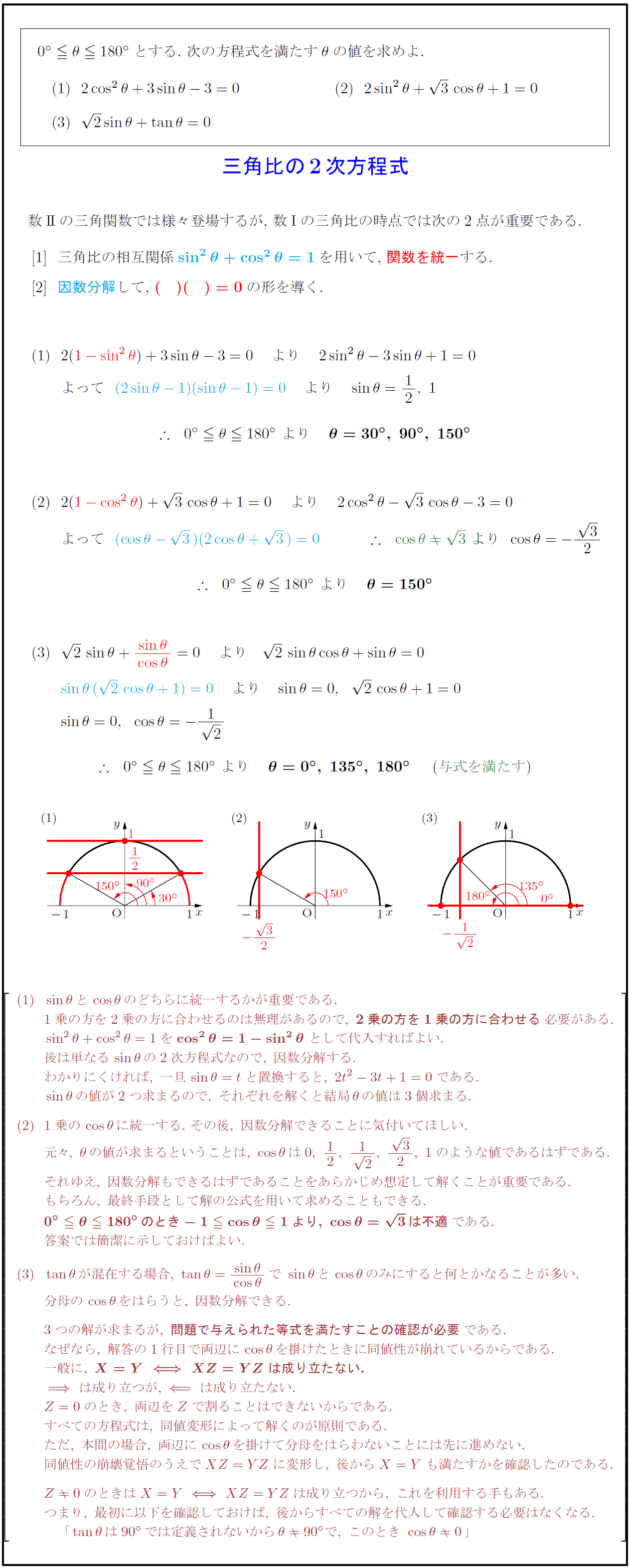
数IIの三角関数では様々登場するが,\ 数Iの三角比の時点では次の2点が重要である. 三角比の相互関係${sin²θ+cos²θ=1$を用いて,\ 関数を統一する. 因数分解して,\ ${( )( )=0$の形を導く. sinθとcosθのどちらに統一するかが重要である. 1乗の方を2乗の方に合わせるのは無理があるので,\ {2乗の方を1乗の方に合わせる}必要がある. \ として代入すればよい. 後は単なるsinθの2次方程式なので,\ 因数分解する. わかりにくければ,\ 一旦sinθ=tと置換すると,\ 2t²-3t+1=0である. sinθの値が2つ求まるので,\ それぞれを解くと結局θの値は3個求まる. 1乗のcosθに統一する.\ その後,\ 因数分解できることに気付いてほしい. 元々,\ θの値が求まるということは,\ cosθは0,\ 12,\ {1}{2},\ {3}{2},\ 1のような値であるはずである. それゆえ,\ 因数分解もできるはずであることをあらかじめ想定して解くことが重要である. もちろん,\ 最終手段として解の公式を用いて求めることもできる. {0°θ180°のとき-1cosθ1より,\ cosθ=3は不適}である. 答案では簡潔に示しておけばよい. tanθが混在する場合,\ tanθ={sinθ}{cosθ}で\ sinθとcosθのみにすると何とかなることが多い. 分母のcosθをはらうと,\ 因数分解できる. 3つの解が求まるが,\ {問題で与えられた等式を満たすことの確認が必要}である. なぜなら,\ 解答の1行目で両辺にcosθを掛けたときに同値性が崩れているからである. 一般に,\ {X=YXZ=YZ\ は成り立たない.} \ は成り立つが,は成り立たない. Z=0のとき,\ 両辺をZで割ることはできないからである. すべての方程式は,\ 同値変形によって解くのが原則である. ただ,\ 本問の場合,\ 両辺にcosθを掛けて分母をはらわないことには先に進めない. 同値性の崩壊覚悟のうえでXZ=YZに変形し,\ 後からX=Yも満たすかを確認したのである. Z0のときはX=YXZ=YZは成り立つから,\ これを利用する手もある. つまり,\ 最初に以下を確認しておけば,\ 後からすべての解を代入して確認する必要はなくなる. 「tanθは90°では定義されないからθ90° で,\ このとき\ cosθ0」

