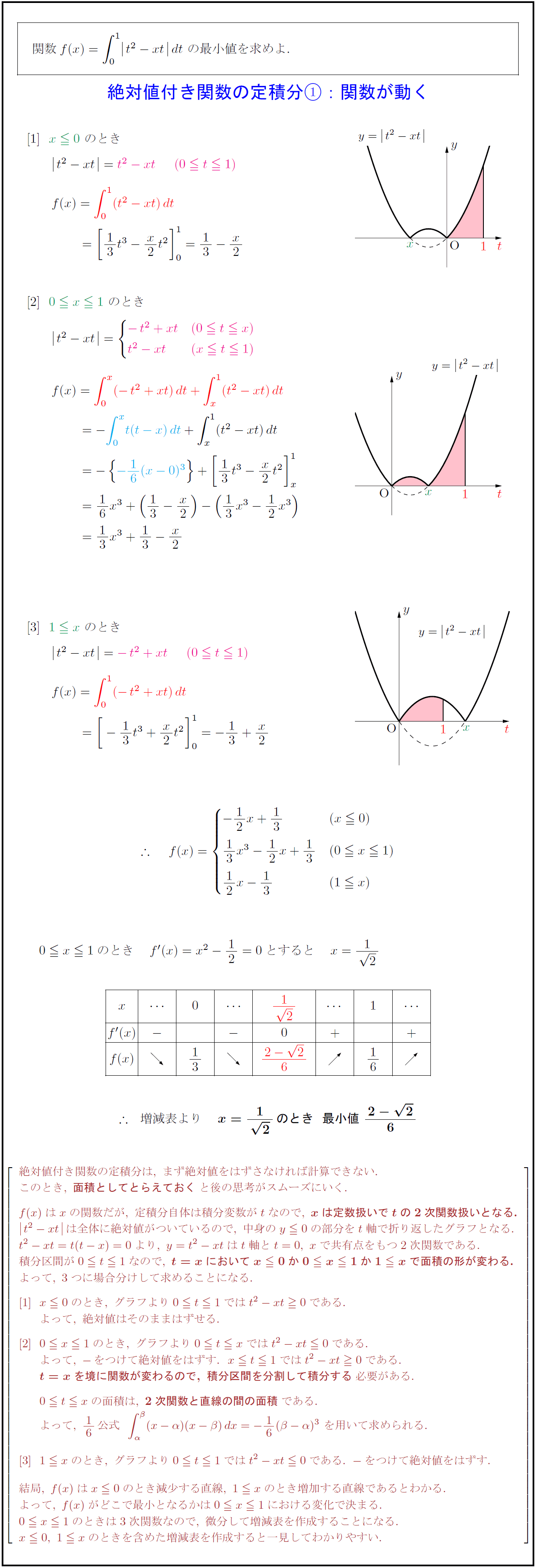
絶対値付き関数の定積分は,\ まず絶対値をはずさなければ計算できない.
このとき,\ 面積としてとらえておく}と後の思考がスムーズにいく.
f(x)はxの関数だが,\ 定積分自体は積分変数がtなので,\ xは定数扱いでtの2次関数扱いとなる.}
t^2-xt}\,は全体に絶対値がついているので,\ 中身のy≦0の部分をt軸で折り返したグラフとなる.
t^2-xt=t(t-x)=0より,\ y=t^2-xtはt軸とt=0,\ xで共有点をもつ2次関数である.
積分区間が0≦ t≦1なので,\ t=xにおいてx≦0か0≦ x≦1か1≦ xで面積の形が変わる.}
よって,\ 3つに場合分けして求めることになる.
[1]\ \ x≦0のとき,\ グラフより0≦ t≦1ではt^2-xt≧0である.
\ \ よって,\ 絶対値はそのままはずせる.
[2]\ \ 0≦ x≦1のとき,\ グラフより0≦ t≦ xではt^2-xt≦0である.
\ \ よって,\ -\,をつけて絶対値をはずす.\ \ x≦ t≦1ではt^2-xt≧0である.
\ \ t=xを境に関数が変わるので,\ 積分区間を分割して積分する}必要がある.
\ \ 0≦ t≦ xの面積は,\ 2次関数と直線の間の面積}である.
\ \ よって,\ 16\,公式\ \ ∫{α}{β}(x-α)(x-β)\,dx=-16(β-α)^3\ を用いて求められる.
[3]}\ \ 1≦ xのとき,\ グラフより0≦ t≦1ではt^2-xt≦0である.\ -をつけて絶対値をはずす.
結局,\ f(x)はx≦0のとき減少する直線,\ 1≦ xのとき増加する直線であるとわかる.
よって,\ f(x)がどこで最小となるかは0≦ x≦1における変化で決まる.
0≦ x≦1のときは3次関数なので,\ 微分して増減表を作成することになる.
x≦0,\ 1≦ xのときを含めた増減表を作成すると一見してわかりやすい.

